0

This question is based on this answer

$Assumptions = {r ∈ Reals, r >= 0, rh ∈ Reals, rh > 0};

S[rh_] := π rh^2
M[rh_, qe_, qm_] = 
  1/2 Sqrt[π/S[rh]] (S[rh]^2/π^2 + S[rh]/π + qe^2 + qm^2) // Simplify;


qe = SolveValues[ϕe == q (1/rh - 1/r), q][[1]] // Simplify;


f[r_, rh_, qm_, ϕe_] = 
  1 + r^2/l^2 - (2 M[rh, qe, qm])/r + (qe^2 + qm^2)/r^2 // Simplify;


G[rh_, qm_, ϕe_] = 
  1/(4 π^2) Sqrt[π/S[rh]] (3 π^2 qm^2 - 
      S[rh]^2 + π S[rh] (1 - ϕe^2)) // Simplify;


T[rh_, qm_, ϕe_] = (-π^2 qm^2 + 
      3 S[rh]^2 + π (S[rh] - S[rh] ϕe^2))/(4 (π S[rh])^(3/2)) // 
   Simplify;


Veff[r_] = f[r, rh, qm, ϕe] (L^2/r^2 + 1) // FullSimplify;


eqn = L^2 == (r0^3 D[f[r0, rh, qm, ϕe], r0])/(2 f[r0, rh, qm, ϕe] - 
        r0 D[f[r0, rh, qm, ϕe], r0]) /. r -> r0 // FullSimplify;


sol = Block[{l = 1, L = 20, ϕe = 3/5}, Solve[eqn, r0, Reals]];


l = 1; L = 20; ϕe = 3/5;


λ[rh_, qm_, ϕe_] = 
  1/2 Sqrt[(r0 D[f[r0, rh, qm, ϕe], r0] - 2 f[r0, rh, qm, ϕe]) *
   Veff''[r0]] /. r -> r0 /. sol // Simplify;


Off[General::munfl, Less::nord]

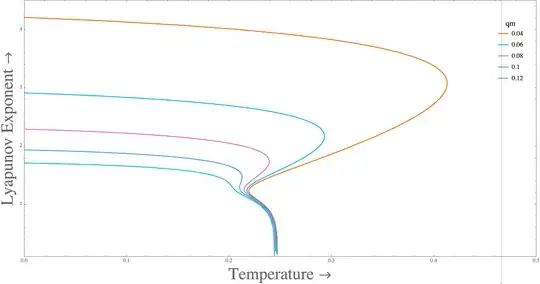
which I tried to generalize for multiple values of qm by using the standard method of creating a Table before plotting:

ParametricPlot[
 Evaluate@
  Table[{T[rh, qm, ϕe], #} & /@ (λ[rh, 
       qm, ϕe][[{3, 5}]]), {qm, 0.04, 0.12, 0.02}], {rh, 0.01, 
  8}, PlotRange -> {{0, 0.5}, {0.1, 4.5}}, AspectRatio -> 0.5, 
 Exclusions -> All]

but unfortunately, it gives me a blank plot. Probably my use of a Table is erroneous when a map is being applied. Any help in this regard would be truly beneficial!

codebpr
  • 2,233
  • 1
  • 7
  • 26
  • 4
    Please share the definition of T and other parameters, so we can run the code. It may also help if you remove the formatting niceties if they are not relevant to the problem. They just clutter the code up and may mask an otherwise obvious issue. – MarcoB May 04 '23 at 14:25
  • @MarcoB Thank you for the useful suggestions. I have edited my question keeping those in mind. – codebpr May 04 '23 at 15:35

1 Answers1

2

Using the definitions from your earlier question.

Flatten the output of your Table.

PlotPoints of 300 is excessive (unnecessary slows down the plot); just use the default.

Including qm = for each legend entry just adds clutter. I recommend that you use LegendLabel.

There are two entries for each value of qm so the colors don't align with the values. Manually set the colors in the legend. (I added Tooltip to aid in this process)

ParametricPlot[Evaluate@
  Flatten[
   Table[
    Tooltip[{T[rh, qm, ϕe], #}, StringForm["qm = ``", qm]] & /@
     (λ[rh, qm, ϕe][[{3, 5}]]),
    {qm, 0.04, 0.12, 0.02}],
   1],
 {rh, 0.01, 8},
 PlotRange -> {{0, 0.5}, {0.1, 4.5}},
 AspectRatio -> 0.5,
 Exclusions -> All,
 PlotTheme -> {"Scientific", "NeonColor"},
 FrameLabel -> {Style["Temperature \[Rule]", FontSize -> 31],
   Style["Lyapunov Exponent \[Rule]", FontSize -> 31]},
 PlotLegends -> Placed[
   LineLegend[
    {RGBColor[1., 0.4, 0.], RGBColor[0., 0.742291, 0.873126], 
     RGBColor[0.893126, 0.4, 0.767184], RGBColor[
     0.238758, 0.610466, 1.], RGBColor[0.295048, 0.8, 0.286932]},
    Range[0.04, 0.12, 0.02],
    LegendLabel -> Style["qm", 14]],
   {0.95, 0.8}],
 ImageSize -> 1000]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198