1

I am using Mathematica for a long calculation, while performing checks throughout the code. I noticed that the following is not working as I expected and is resulting in inconsistencies later on.

Simplify[(b + c)/a, {a + b + c == 0}, Assumptions -> {Reals[a, b, c], a != 0, b != 0, c != 0}]

(* Out: (b + c)/a *)

I have also tried FullSimplify and Refine, but nothing seems to return the answer $-1$. Can someone point out what needs to be added/changed to obtain the expected result and/or why this does not automatically Simplify to $-1$?

I suspect there is a similar problem in the following as well:

FullSimplify[
  (b/c)^n/a^n - (b/(a*c))^n, 
  Assumptions -> {
    Reals[a, b, c], Integers[n], 
    a != 0, b != 0, c != 0, 
    n > 1
  }
]

(* Out: (b/c)^n/a^n - (b/(ac))^n )

I am using Mathematica 12.2

MarcoB
  • 67,153
  • 18
  • 91
  • 189
Lelouch
  • 237
  • 2
  • 7
  • 1
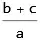
    Your second FullSimplify simply suffers from a syntax error: Reals is a domain, not a function, so you should write Element[{a, b, c}, Reals] instead of Reals[a, b, c]. The latter means nothing. With those changes, the expression simplifies to zero. – MarcoB May 06 '23 at 11:17

2 Answers2

3

side relation is little tricky. See Why does side relation work differently in these two cases?

For your case it works if you do this

ClearAll[a, b, c]
Simplify[(b + c)/a, {b + c == -Unevaluated[a]}]
(* -1 *)

Compare to

Simplify[(b + c)/a, {b + c == -a}]

Mathematica graphics

And

Simplify[(b + c)/a, {b + c + a == 0}]

Mathematica graphics

Nasser
  • 143,286
  • 11
  • 154
  • 359
3

For the first case:

(b + c)/a /. b -> -a - c

or any equivalent phrasal of the relation should suffice.

For the second case:

expr = (b/c)^n/(a)^n - (b/(a*c))^n

PowerExpand[expr] gives 0.

or try:

Simplify[expr, TransformationFunctions -> {Automatic, PowerExpand}]

or improve syntax:

Simplify[expr, 
 Assumptions -> {{a, b, c} ∈ Reals, n ∈ Integers, 
   a != 0, b != 0, c != 0, n > 1}]
Syed
  • 52,495
  • 4
  • 30
  • 85