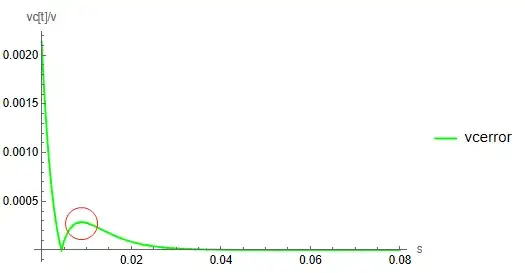
What instruction could I use to obtain the local maximum point of the red circle in the graph? I tried using the $FindMaximum$ instruction, but couldn't get the desired result.
The curve generation code is as follows:
dt = 0.00006;
tend = 0.08;
sol = DSolve[{l il'[t] == vl[t], c vc'[t] == ic[t],
ir[t] == -ic[t] + il[t], vl[t] == 24 - vc[t], vr[t] == vc[t],
vr[t] == r ir[t], il[0] == 0, vc[0] == 0}, {ir[t], il[t], ic[t],
vr[t], vl[t], vc[t]}, t];
{il[t_], vc[t_]} = {il[t], vc[t]} /. sol[[1]];
pars1 = {r -> 22, l -> 1/5, c -> 1/10000};
a = Evaluate[vc[t] /. pars1];
dvc = D[a, t];
Subscript[dvc, n + 1] = ReplaceAll[dvc, t -> t + dt];
vcerror = Abs[-1/2*dt*(Subscript[dvc, n + 1] - dvc)];
Plot[{vcerror}, {t, 0, tend}, AxesLabel -> {"s", "vc[t]/v"},
PlotLegends -> {"vcerror"}, PlotStyle -> {Green}, PlotRange -> All]
NMaximize[{vcerror, 0 <= t <= tend}, t]
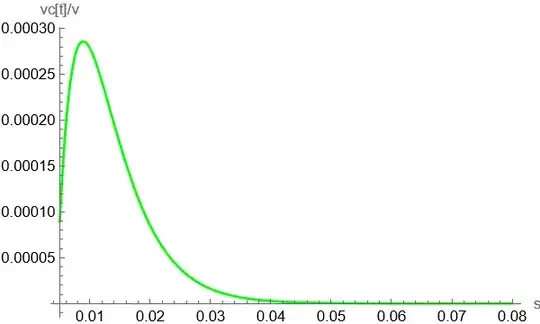
NMaximize[{vcerror, 0.01 < t < 0.02}, t]– Daniel Huber May 11 '23 at 09:30