Obtaining better Fourier series for a piecewise constant function

Question

I have the give wave-train:

and I extract the given set of points:

points = {{496.04173755848626`, 
    257.544927690344`}, {487.67960442364995`, 
    290.993460229689`}, {474.30019140791205`, 
    319.42471288813226`}, {465.93805827307574`, 
    381.3044980859205`}, {454.23107188430504`, 
    296.01074011059075`}, {449.2137920034032`, 
    227.4412484049335`}, {435.8343789876652`, 
    406.3908974904292`}, {429.1446724797962`, 
    324.441992769034`}, {422.4549659719272`, 
    225.7688217779663`}, {419.1101127179927`, 
    292.66588685665624`}, {405.7306997022548`, 
    408.06332411739646`}, {402.3858464483203`, 
    341.16625903870647`}, {395.6961399404513`, 
    200.68242237345748`}, {392.3512866865168`, 
    294.3383134836235`}, {389.0064334325823`, 
    413.0806039982982`}, {378.9718736707788`, 
    319.42471288813226`}, {378.9718736707788`, 
    314.4074330072305`}, {368.9373139089753`, 
    237.475808166737`}, {357.2303275202046`, 
    403.0460442364947`}, {345.52334113143377`, 
    284.30375372182`}, {340.50606125053207`, 
    334.47655253083747`}, {335.48878136963026`, 
    232.4585282858353`}, {322.10936835389225`, 
    399.70119098256026`}, {315.41966184602325`, 
    322.76956614206676`}, {300.36782220331804`, 
    244.16551467460602`}, {292.00568906848184`, 
    324.441992769034`}, {285.31598256061284`, 
    396.35633772862576`}, {275.28142279880933`, 
    317.752286261165`}, {265.2468630370058`, 
    224.096395150999`}, {256.8847299021695`, 
    401.37361760952746`}, {245.17774351339884`, 
    324.441992769034`}, {241.83289025946434`, 
    212.3894087622283`}, {223.43619736282457`, 
    332.8041259038703`}, {218.41891748192282`, 
    473.2879625691192`}, {216.74649085495557`, 
    322.76956614206676`}, {205.0395044661848`, 
    178.94087622288328`}, {195.0049447043813`, 372.94236495108424`}};

I generate a piecewise constant function by the command:

    Clear[t];
    f[t_] = Piecewise[
       Partition[Sort[points], 2, 
         1] /. {{a_?NumericQ, b_}, {c_, d_}} :> {b, a <= t < c}];
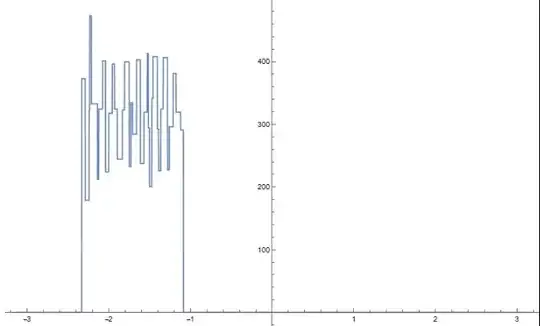
f1[t_] = f[(758.6127179923444` (t + Pi)/Pi)];
Plot[f1[t], {t, -Pi, Pi}]

which is shown below:

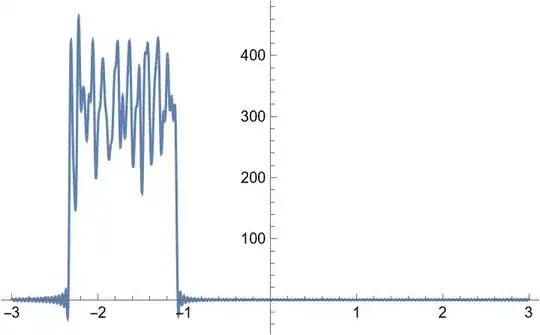
However, the Fourier transform gives a disappointing set of peaks that do not reflect the waves related to those points, which we can see the peaks in each interval of the piecewise constant function:

FD[t_] = FourierSeries[f1[t], t, 15];
Plot[{FD[t]}, {t, -3, 3}, PlotRange -> Full]

Increasing the number of Fourier terms, from 15 to 20, does not make things very different. And reducing them, also makes no difference.

Is anyone aware of a way we can get a Fourier series which has a higher number of peaks that is more similar to the peaks of the piecewise constant function?

Can the spacing between each interval be increased? I tried changing the resolution of the original image of the waves where I got those points from, but the plot is always the same.

Thanks

Your objective is not clear. If you just want a spectrum then Fourier will give you the spectrum very quickly. The spectrum is the amplitude of the sines and cosines that make up your data. You may have to interpolate and get even spacing first. Notes on Fourier here. If you just want the lower frequencies and fewer sines and cosines then you can filter first. — Hugh, May 12 '23 at 11:06

score 3 · Answer 1 · answered May 12 '23 at 09:07

3

A jump contains arbitrary high frequencies. Further, there is the Gibbs phenomenon, that says that there will be wiggles for any number of Fourier series terms, for higher number of terms, the wiggles will be closer together and will not become infinite small.

To give an example I choose a simpler function f that takes less time to get compute the Fourier series:

fun[t_]= HeavisideTheta[t] - HeavisideTheta[t - 1];
Plot[fun[t],{t,-1,2},PlotStyle->Red]

Do[
 FD[t_] = FourierSeries[fun[t], t, i];
 Plot[{FD[t]}, {t, -3, 3}, PlotRange -> Full] // Print
 , {i, 10, 60, 10}]

answered May 12 '23 at 09:07

Daniel Huber

51,463
1
23
57

So there is no chance of getting a real wave set like in the picture i put now in the OP= – Vangsnes May 12 '23 at 09:11
1

A jump will always create wiggles. If you do not want wiggles, then the slope must nowhere be infinite. – Daniel Huber May 12 '23 at 09:19
So generating a piecewise constant function is not a good idea? – Vangsnes May 12 '23 at 09:20
1

For a Fourier series-- NO – Daniel Huber May 12 '23 at 10:30
Are you aware of other alternatives than piecewise constant functions? – Vangsnes May 12 '23 at 10:33
1

What about "Interpolation" ? – Daniel Huber May 12 '23 at 10:55
Right, but you don't get an analytic function that you can "play" with (ie. with operators) using interpolation – Vangsnes May 12 '23 at 10:57
Yes, the Wilbraham-Gibbs phenomenon (Google-able) gives a somewhat-disappointing, but interesting, limitation about how well the Fourier series can approximate a function at jumps. – paul garrett May 12 '23 at 18:19

score 2 · Accepted Answer · answered May 12 '23 at 09:42

2

FD[t_] = FourierSeries[f1[t], t, 150];
Plot[{FD[t]}, {t, -3, 3}, PlotRange -> Full]

Its execution on my comp takes approximately an hour.

answered May 12 '23 at 09:42

user64494

26,149
4
27
56

Thanks user! This was much better than I thought was possible. I will use this method. – Vangsnes May 12 '23 at 09:46

score 2 · Answer 3 · answered May 12 '23 at 13:13

2

With such a function, remember the numerical calculation of the Fourier series. Execution time in this case 1 minute.

<< FourierSeries`
FD[t_] = NFourierSeries[f1[t], t, 150];
Plot[{FD[t]}, {t, -3, 3}, ImageSize -> Medium]

answered May 12 '23 at 13:13

rmw

1,950
6
9

Do you get an analytic function out of this? – Vangsnes May 12 '23 at 13:17
1

Ok, it's a polynomial with 150 terms. If you want a trig function, add FD[t]//ExpToTrig. – rmw May 12 '23 at 13:39
Weird, Ican't get that numerical form of the fourier series to work at all – Vangsnes May 12 '23 at 14:28

Obtaining better Fourier series for a piecewise constant function

3 Answers3