Create a new graph based on a manipulated circle

Question

I make a circle based on CirclePoints. From this list of points I take a part and rotate the coördinaties. Then I join the rotated part with the rest of the circelPoints.

For example

crcl = Graphics[Line[CirclePoints[360]]];
data = Take[CirclePoints[360], {90, 180}];

I Rotate this part of the circle and combines it with the rest of the original circle

datacrcl = Flatten[{Take[CirclePoints[360], {1, 90}], 
  MapAt[RotationTransform[
      180 Degree, {(First[data][[1]] + Last[data][[1]])/
        2 , (First[data][[2]] + Last[data][[2]])/2}][#] &, data, 
   Position[data, {_, _}]],
  Take[CirclePoints[360], {180, 360}]
  }, 1];

I want to plot this list for example as BSlinecurve.

Graphics[BSplineCurve[datacrcl]]

I Want the output like

I tried different options using functions like

FindCurvePath
FindShortestTour

But non of them was usefull to get the desired output. Who has a suggestion for my problem?

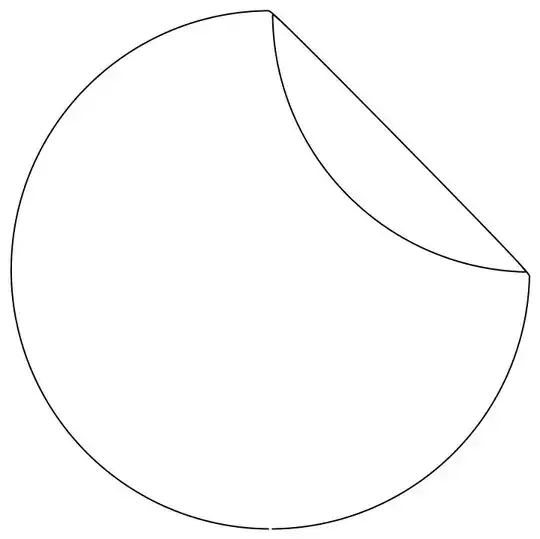
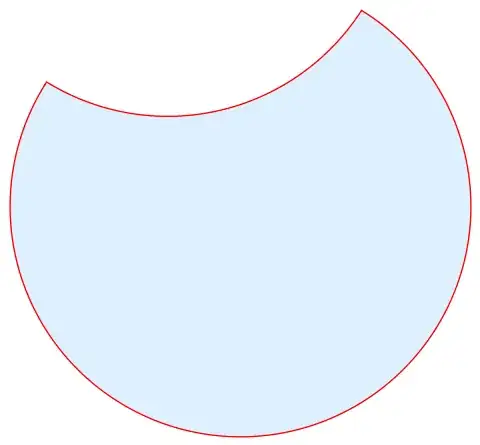
"Manipulated" is a poor choice of words here, since your question has nothing to do with Manipulate. — David G. Stork, May 15 '23 at 15:37

cvgmt · Answer 1 · 2023-05-15T14:54:54.160

4

reg = datacrcl // Polygon // Graphics // BoundaryDiscretizeGraphics //
    RegionBoundary;
Graphics[{PointSize[0], Red, reg}]
RegionPlot[reg]
Region[reg]

edited May 15 '23 at 14:54

answered May 15 '23 at 14:49

cvgmt

72,231
4
75
133

you can replace // Graphics // BoundaryDiscretizeGraphics with BoundaryDiscretizeRegion – kglr May 15 '23 at 17:01

score 4 · Answer 2 · answered May 15 '23 at 15:24

You should be more clear about the format that you want to work with. If you literally just want the visualization, then there are many ways to get there. It's also not clear how general you want this to be. Will you want to display different amounts of cutaway? Here's an approach that works with regions instead of points. I've generalized slightly.

EclipsedDisk[shadowSpan : {a_, b_}] :=
  With[
    {mid = Mean[{{Cos[a], Sin[a]}, {Cos[b], Sin[b]}}]},
    RegionDifference[Disk[], Disk[2 mid]]]

For your specific example:

RegionPlot[EclipsedDisk[{0, Pi/2}]]

Or if you want just the boundary (using a different example):

Region[RegionBoundary[EclipsedDisk[{Pi/4, 7 Pi/8}]]]

Once you have the region, you could discretize it, extract points, etc.

Going back to your original attempt, the reason why you had that straight edge in your output was because of the order of the points. Once you rotated those points, you ended up with a gap when you just followed them in order with Line or BSplineCurve. You could have added a Reverse in there or you could have used a ReflectionTransform instead of RotationTransform. So, to be specific, change your definition for datacrcl like this:

datacrcl = 
  Flatten[
    {Take[CirclePoints[360], {1, 90}], 
     Reverse@MapAt[
       RotationTransform[...same computation...], data,  Position[data, {_, _}]], 
     Take[CirclePoints[360], {180, 360}]}, 
    1]

I made another small change. I removed the "[#]&", which was unnecessary, since RotationTransform will generate a function. There are other simplifications you could make to this code, but I didn't want to mutate it too much.

kglr · Accepted Answer · 2023-05-16T21:53:38.637

If you have to work with CirclePoints:

Specify the starting angle (start) and break CirclePoints[{1, start}, 360] into two pieces with lengths deg (length in degrees of the desired arc) and 360 - deg using TakeDrop:

arcPieces[deg_, start_ : 0] := TakeDrop[CirclePoints[{1, start}, 360], deg]

Using the idea/code from this answer by J.M. to reflect points through the line passing through the points {p1, p2}:

reflectThrough[{p1_, p2_}] := 2 p1 + 2 Projection[# - p1, p2 - p1] - # &;

Apply reflectThrough to the first part of arcPieces to get the desired coordinate list:

arcCoords = Apply[Join[reflectThrough[#[[{-1, 1}]]] /@ #, #2] &] @* arcPieces;

Examples:

Graphics[{EdgeForm[Red], FaceForm[LightBlue], Polygon @ arcCoords[90]}]

Start from 45 Degree:

Graphics[{ EdgeForm[Red], FaceForm[LightBlue], Polygon @ arcCoords[90, 45]}]

If deg > 180 the reflection of the cut piece falls outside the original circle:

Graphics[{Gray, Circle[], 
  EdgeForm[Red], FaceForm[LightBlue], 
  Polygon @ arcCoords[240]}]

SeedRandom[1];
Graphics[Table[With[{i = i, j = j},

  {EdgeForm[Red], FaceForm[RandomColor[]], 
   Polygon @ TranslationTransform[{5/2 i, 5/2 j}] @
    arcCoords[RandomInteger[{0, 180}], RandomInteger[{0, 360}]]}], 
  {i, 5}, {j, 5}], ImageSize -> Large]

SeedRandom[7];
Graphics[Table[With[{i = i, j = j}, 
  {Gray, Circle[{5 i, 5 j}], 
   EdgeForm[Red], FaceForm[RandomColor[]], 
   Polygon@TranslationTransform[{5 i, 5 j}]@
      arcCoords[RandomInteger[{180, 360}], 
       RandomInteger[{0, 360}]]}], {i, 5}, {j, 5}], 
 ImageSize -> Large]

Create a new graph based on a manipulated circle

3 Answers3