How can I interpolate a piecewise constant function?

Question

Let the given set of points

points = {{395.4416644777464`, 
    207.63931734339303`}, {391.15890276860114`, 
    240.47382378017346`}, {382.59337935031067`, 
    219.06001523444706`}, {378.3106176411653`, 
    209.0669045797748`}, {369.74509422287485`, 
    177.65998537937617`}, {361.1795708045843`, 
    250.4669344348457`}, {355.46922185905726`, 
    204.78414287062958`}, {346.9036984407667`, 
    236.19106207102823`}, {341.19334949523966`, 
    184.79792156128497`}, {332.6278260769492`, 
    220.48760247082885`}, {326.9174771314222`, 
    214.77725352530183`}, {322.6347154222768`, 
    260.4600450895181`}, {316.9243664767498`, 
    219.06001523444706`}, {314.06919200398636`, 
    241.90141101655524`}, {304.076081349314`, 
    119.12890868772422`}, {295.5105579310235`, 
    327.5566451994606`}, {278.3795110944425`, 
    156.24617683364988`}, {269.8139876761519`, 
    251.8945216712275`}, {264.1036387306249`, 
    196.218619452339`}, {258.39328978509786`, 
    286.1566153443896`}, {249.8277663668073`, 
    233.33588759826466`}, {241.26224294851679`, 
    173.37722367023093`}, {231.26913229384448`, 
    184.79792156128497`}, {224.13119611193568`, 
    286.1566153443896`}, {215.56567269364515`, 
    160.52893854279512`}, {199.86221309344583`, 
    303.28766218097076`}, {184.1587534932465`, 
    72.01852988712619`}, {172.73805560219247`, 
    587.3775222209401`}, {162.74494494752017`, 
    83.43922777818022`}, {149.89665982008435`, 
    260.4600450895181`}, {145.61389811093912`, 
    254.74969614399106`}, {138.47596192903032`, 
    317.56353454478824`}, {131.33802574712158`, 
    183.37033432490318`}, {124.20008956521278`, 
    193.36344497957543`}, {119.91732785606749`, 
    160.52893854279512`}, {112.77939167415872`, 
    214.77725352530183`}, {108.49662996501345`, 
    199.07379392510256`}, {105.64145549224995`, 
    250.4669344348457`}, {101.35869378310466`, 
    324.70147072669704`}, {98.50351931034115`, 
    224.77036417997408`}, {91.36558312843238`, 
    220.48760247082885`}, {81.37247247376007`, 
    96.28751290561604`}, {75.66212352823305`, 
    200.50138116148423`}, {72.80694905546954`, 
    351.82562821795045`}, {54.24831498250671`, 
    154.8185895972681`}, {41.4000298550709`, 
    240.47382378017346`}, {35.68968090954388`, 
    236.19106207102823`}, {32.83450643678037`, 
    280.4462663988626`}, {12.848285127435787`, 
    131.97719381515992`}, {7.1379361819087705`, 227.62553865273765`}};

define the coordinates for the piecewise constant function generated as such:

points2 = {#[[1]], #[[2]] - 72.01852988712619`} & /@ points;
Clear[t];
f[t_] = Piecewise[
   Partition[Sort[points2], 2, 
     1] /. {{a_?NumericQ, b_}, {c_, d_}} :> {b, a <= t < c}];
f1[t_] = f[(172.73805560219247` (t + Pi)/Pi)];
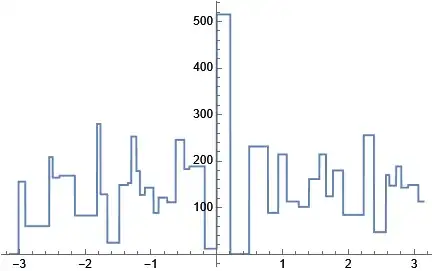
Plot[f1[t], {t, -Pi, Pi}]

Then we obtain the plot

However, I would like to generate an interpolation of this function, I tried

Interpolation[f1[t]]

But got

Interpolation::innd: First argument in Piecewise[{{155.607,7.13794<=54.9842 ([Pi]+t)<12.8483},{59.9587,12.8483<=54.9842 ([Pi]+t)<32.8345},{208.428,32.8345<=54.9842 ([Pi]+t)<35.6897},{164.173,35.6897<=54.9842 ([Pi]+t)<41.4},{168.455,41.4<=54.9842 ([Pi]+t)<54.2483},{82.8001,54.2483<=54.9842 ([Pi]+t)<72.8069},{279.807,72.8069<=54.9842 ([Pi]+t)<75.6621},{128.483,75.6621<=54.9842 ([Pi]+t)<81.3725},{24.269,81.3725<=54.9842 ([Pi]+t)<91.3656},{148.469,91.3656<=54.9842 ([Pi]+t)<98.5035},<<39>>},0] does not contain a list of data and coordinates."

I tried also to interpolate the Fourier series of this function:

Interpolate[FD[t_] = FourierSeries[f1[t], t, 20]]

However, I am not sure this is the best way to do it.

Any ideas?

Thanks

Possible duplicate: https://mathematica.stackexchange.com/questions/30055/how-can-the-behavior-of-interpolationorder-0-be-controlled — Michael E2, May 17 '23 at 00:34

score 3 · Answer 1 · answered May 16 '23 at 08:46

3

For functions your can directly use FunctionInterpolation[ ] like this

fInterpol = 
 FunctionInterpolation[f1[t], {t, -Pi, Pi}, InterpolationOrder -> 1, 
  InterpolationPoints -> 300]
Plot[fInterpol[t], {t, -Pi, Pi}, PlotRange -> All]

answered May 16 '23 at 08:46

Acus

3,669
14
21

Nasser · Accepted Answer · 2023-05-16T08:47:19.577

2

You need to generate the data points. One way is

ClearAll["Global`*"];
points = {{395.4416644777464`, 207.63931734339303`},....} (*same as you have*)
points2 = {#[[1]], #[[2]] - 72.01852988712619`} & /@ points;
f[t_] := Piecewise[Partition[Sort[points2], 2, 
     1] /. {{a_?NumericQ, b_}, {c_, d_}} :> {b, a <= t < c}];
f1[t_] := f[(172.73805560219247` (t + Pi)/Pi)];
Plot[f1[t], {t, -Pi, Pi}]

Mathematica graphics

And now

intep = Interpolation[Table[{t, f1[t]}, {t, -Pi, Pi, Pi/100}], InterpolationOrder -> 1]

Mathematica graphics

Plot[intep[t], {t, -Pi, Pi}]

Mathematica graphics

You can modify InterpolationOrder or the granulaity of data generated to make improvement as needed.

edited May 16 '23 at 08:47

answered May 16 '23 at 08:29

Nasser

143,286
11
154
359

Thanks Nasser! This is great. – Vangsnes May 16 '23 at 08:35
it appears that the interpolating function can be used in a system of algebraic equations, to solve for unknown parameters. – Vangsnes May 16 '23 at 12:39

How can I interpolate a piecewise constant function?

2 Answers2