Weierstrass substitution \[Alpha] -> 2 ArcTan[u] gives the solution
eq = Tan[2 \[Alpha]] ==Cos[\[Alpha]]/(2 - Sin[\[Alpha]]) /. \[Alpha] -> 2 ArcTan[u] // TrigExpand // Simplify
(*1/2 (-1 + u^2) (1/(1 - u + u^2) - (8 u)/(1 - 6 u^2 + u^4)) == 0*)
solu=Solve[eq, u] (* four solutions! )
({{u -> -1}, {u -> 1}, {u -> 4 - Sqrt[15]}, {u -> 4 + Sqrt[15]}}*)
alfa=Tan[2 ArcTan[u]] /. solu // TrigExpand // Simplify
(* {-([Pi]/2), [Pi]/2, 2 ArcTan[4 - Sqrt[15]], 2 ArcTan[4 +Sqrt[15]]} *)
Plot[{Tan[2 [Alpha]],Cos[[Alpha]]/(2 - Sin[[Alpha]])}, {[Alpha], -Pi, Pi},GridLines -> { alfa , None}]
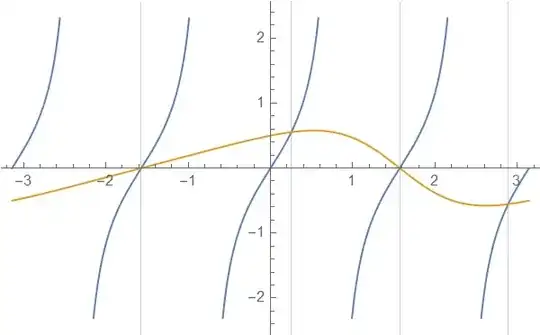
result Tan[\[Alpha]]
Map[Tan,alfa]
(*{ComplexInfinity, ComplexInfinity, Tan[2 ArcTan[4 - Sqrt[15]]],Tan[2 ArcTan[4 + Sqrt[15]]]}*)

Cos[\[Alpha]]/(2 - Sin[\[Alpha]]), t == Sin[\[Alpha]]/Cos[\[Alpha]], 0 < \[Alpha] < \[Pi]/2}, t, {Sin[\[Alpha]], Cos[\[Alpha]]}]```The result calculated in this way is also incorrect– csn899 May 16 '23 at 14:19Solve[{TrigExpand[Tan[2 α]] == Cos[α]/(2 - Sin[α]), tanα == Sin[α]/Cos[α], 0 < α < π/2}, tanα, {Sin[α], Cos[α]}, MaxExtraConditions -> All]orReduce[{TrigExpand[Tan[2 α]] == Cos[α]/(2 - Sin[α]), tanα == Sin[α]/Cos[α], 0 < α < π/2}, tanα]. Why it should be is explained in What is the difference between Reduce and Solve? – Artes May 16 '23 at 14:20{}in 13.2.1 on Windows 10. – user64494 May 16 '23 at 14:25Solve. – Artes May 16 '23 at 14:28tan\[Alpha] -> ConditionalExpression[Tan[\[Alpha]], 0 < \[Alpha] < \[Pi]/2]the answer is incorrect – csn899 May 16 '23 at 14:31{}. – user64494 May 16 '23 at 14:44Solve. It works correctly. You haven't read the link I provided. All what you need can be found there. – Artes May 16 '23 at 14:48Out[129]= {-c (c^2 - 4 s + s^2), -s + c tan, -1 + c^2 + s^2}
In[131]:= Solve[tpolys == 0, tan, {c, s}]
Out[131]= {{tan -> -(1/Sqrt[15])}, {tan -> 1/Sqrt[15]}}`
– Daniel Lichtblau May 16 '23 at 15:19