How to wrap a cylinder?

Question

i'm trying to wrap a cylinder in a torus, the best i've done is the following code:

Manipulate[ParametricPlot3D[{(2 + Cos[v]) Cos[u/(6 - gamma)] - 2, (2 + Cos[v]) Sin[u/(6 - gamma)], Sin[v] + 1}, {u, 0, 2 Pi}, {v,0, 2 Pi},
ImageSize -> 500, Mesh -> None, BoxRatios -> {2, 1, 1}, PlotRange -> {{-2 \[Pi], 2 \[Pi]}, {-6, 2 \[Pi]}, {0, 4}}, PlotStyle -> Directive[Opacity[0.5], Blue], 
BoundaryStyle -> Directive[Black, Opacity[.3]]], {{gamma, 1,"gamma"}, 1, 5}]

but I would like to start with a cylinder and not with a piece of the torus

Does it fit you needs? https://mathematica.stackexchange.com/q/42493/5478 — Kuba, May 17 '23 at 05:20

cvgmt · Accepted Answer · 2023-05-21T14:15:54.710

At first we wrap a line to circle.

With[{L = 30}, 
 Manipulate[
  ParametricPlot3D[{0, R, 0} + 
    R {Cos[t], Sin[t], 0}, {t, -π/
     2 - (L/2)/R, -(π/2) + (L/2)/R}, PlotRange -> L/2], {R, 200, 
   L/(2 π)}]]

Then we wrap the cylinder.

Clear["Global`*"];
L = 30; r = 1;
f[R_, t_] = {0, R, 0} + R {Cos[t], Sin[t], 0};
{n[R_, t_], b[R_, t_]} = FrenetSerretSystem[f[R, t], t][[2]][[2 ;; 3]];
Manipulate[
 ParametricPlot3D[{0, R, 0} + R {Cos[t], Sin[t], 0} + 
   r*{Cos[s], Sin[s]} . {n[R, t], b[R, t]}, {t, -(π/2) - (L/2)/
     R, -(π/2) + (L/2)/R}, {s, 0, 2 π}, 
  PerformanceGoal -> "Quality", PlotRange -> L/2, Boxed -> False, 
  Axes -> False], {R, 200, L/(2 π)}]

Edit

Since the curvature of the circle is κ=1/R where R is the radio of the circle, we replace all of the 1/R to κ then make the animation smoothly.

With[{L = 30, R = 1/κ}, 
 Manipulate[
  ParametricPlot[{0, R} + 
    R {Cos[t], Sin[t]}, {t, -π/2 - (L/2)/R, -(π/2) + (L/2)/R},
    PlotRange -> L/2], {κ, 10^-10, 2 π/L}]]

Clear["Global`*"];
L = 30; r = 1;
f[R_, t_] = PadRight[{0, R} + R {Cos[t], Sin[t]}, 3];
{n[R_, t_], b[R_, t_]} = FrenetSerretSystem[f[R, t], t][[2, 2 ;; 3]];
Manipulate[
 Block[{R = 1/κ}, 
  ParametricPlot3D[
   f[R, t] + 
    r*{Cos[θ], Sin[θ]} . {n[R, t], b[R, t]}, {t, -π/
      2 - (L/2)/R, -(π/2) + (L/2)/R}, {θ, 0, 2 π}, 
   PerformanceGoal -> "Quality", PlotRange -> L/2, Boxed -> False, 
   Axes -> False, Lighting -> "ThreePoint"]], {κ, 10^-10, 
  2 π/L}]

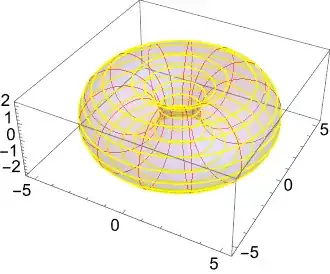
Wrap a rectangle to a torus.

Clear["Global`*"];
L = 95; l = 30;
list1 = Table[
   Block[{R = 1/κ}, 
    ParametricPlot3D[{0, 0, R} + 
      R {0, Cos[t], Sin[t]} + {s, 0, 0}, {t, -π/2 - 
       l/2/R, -π/2 + l/2/R}, {s, -L/2, L/2}, 
     PerformanceGoal -> "Quality", PlotRange -> L/2, Boxed -> False, 
     Axes -> False]], {κ, Subdivide[10^-10, 2 π/l, 10]}];
f[R_, t_] = {0, R, 0} + R {Cos[t], Sin[t], 0};
{n[R_, t_], b[R_, t_]} = FrenetSerretSystem[f[R, t], t][[2, 2 ;; 3]];
list2 = Table[
   Block[{R = 1/κ, r = l/2/π}, 
    ParametricPlot3D[
     f[R, t] + {0, 0, r} + 
      r*{Cos[θ], Sin[θ]} . {n[R, t], 
         b[R, t]}, {t, -π/2 - (L/2)/R, -(π/2) + (L/2)/
        R}, {θ, 0, 2 π}, PerformanceGoal -> "Quality", 
     PlotRange -> L/2, Boxed -> False, Axes -> False]], {κ, 
    Subdivide[10^-10, 2 π/L, 20]}];
ListAnimate[Join[list1, list2]]

score 4 · Answer 2 · answered May 16 '23 at 18:10

First set up some helper functions then create polygonFunction that can transform a cylinder into a torus via RotationTransform. Also generate some axes for visualization:

myxf[alpha_, phi_] := (R + \[Rho] Cos[alpha]) Cos[phi];
myyf[alpha_, phi_] := (R + \[Rho] Cos[alpha]) Sin[phi];
myzf[alpha_, phi_] := \[Rho] Sin[alpha];
R = 2;
\[Rho] = 1
myaeta[[Eta]_] := 2 ArcTan[Sqrt[3] Tan[(Sqrt[3] [Eta])/2]];
rhoMax = NIntegrate[1/(2 + Cos[a]), {a, 0, [Pi]}];
myx = [Pi]/(0.001 rhoMax) Sin[0.001];
newval = 1/(myx - 1)
resol = 0.1;
polygonFunction = 
  Outer[Compose, 
   Table[RotationTransform[
     a Pi/l2, {0, 0, 1.}, {-l2 + 1, 0, 0}], {a, -1, 1, resol}], 
   Table[
    theta2 = (ArcTan[myxf[a, b] - 2, myzf[a, b]]/[Pi]) /. {a -> 
        myaeta[theValue], b -> 0};
myalpha = ArcSin[(0.0001 myx theValue)/\[Pi]];
mya = myalpha/0.0001;
newf4 := ((theta2 - mya)/( \[Pi] - 0.0001) (x - 0.0001) + mya);
RotationTransform[(newf4) \[Pi], {0, 1, 
   0}, {3 - 1/(myx - 1/(newval)), 0, 0}][{3, 0, 
  0}], {theValue, -1.8, 1.8, resol}], 1];


etaxiAxes = 
  Graphics3D[
   Map[Line, {{{3, 4, 0}, {3, -4, 0}}, {{3, 0, 4}, {3, 0, -4}}}]];
vAxis = Graphics3D[
   Map[Line, {{{-3, 0, 0}, {3, 0, 0}}, {{0, -3, 0}, {0, 3, 0}}, {{0, 
       0, -3}, {0, 0, 3}}}]];

Now using the variable t2, continuously bend the cylinder into a torus using Manipulate:

Manipulate[
 Show[{Graphics3D@{{EdgeForm[], Polygon[#[[{1, 2, 4, 3}]]]} & /@ 
      Join @@@ (Join @@ 
         Partition[(polygonFunction /. {l2 -> \[Pi]/t2, x -> t2}), {2,
            2}, 1])}, etaxiAxes, vAxis}, PlotRange -> 4, 
  Axes -> True], {t2, 0.001, Pi}]

Static picture below of intermediate form at t2=0.58.

score 4 · Answer 3 · answered May 17 '23 at 04:26

func[r_, a_, d_] := 
 If[d <= r a, r {Sin[d/r], -Cos[d/r], 0}, 
  r {Sin[a], -Cos[a], 0} + (d - r a) {Cos[a], Sin[a], 0}]

Making animated gif:

gi = Table[
   ParametricPlot3D[func[1, a, t], {t, 0, 2 Pi}, 
     PlotRange -> Table[{-2 Pi, 2 Pi}, 3], Boxed -> False, 
     Background -> Black, Axes -> False] /. 
    Line[x__] :> {Red, Tube[x, 0.4]}, {a, 0, 2 Pi, 0.1}];

score 3 · Answer 4 · answered May 16 '23 at 16:02

Do you mean wrap a cylinder into a torus?

torus[gamma_][{u_, v_}] :=
 {(1 + gamma Cos[v]) Cos[u],
  (1 + gamma Cos[v]) Sin[u],
  gamma Sin[v] 
  }
Manipulate[
 ParametricPlot3D[torus[gamma][{u, v}], {u, .0, uUB}, {v, 0, vUB}, 
  PlotRange -&gt; 2.5 {{-1, 1}, {-1, 1}, {-1, 1}}],
 {{gamma, .1}, 0, 1},
 {{uUB, 2 Pi}, .01, 2 Pi},
 {{vUB, 2 Pi}, .01, 2 Pi}


]

Or, wrap a cylinder onto a torus

curve[s_] := Pi { Cos[ s], Sin[s]}
Manipulate[
 ParametricPlot3D[torus[gamma][curve[s]], {s, .0, sUB}, 
   PlotRange -> 2.5 {{-1, 1}, {-1, 1}, {-1, 1}}] /.
  Line[args_] :> Tube[args, .025],
 {{gamma, .1}, 0, 1},
 {{sUB, 2 Pi}, .01, 2 Pi}
]

Or, something else?

Roland F · Answer 5 · 2023-05-16T19:15:53.963

A torus is circle in the 1,2-plane , at each point an orthogonal circle in the r-3 plane with its center on the first circle.

  PolarX[R_, 
   r_, \[Theta]_, \[Phi]_] := {(R + r Sin[\[Theta]]) Cos[\[Phi]], (R + 
    r Sin[\[Theta]]) Sin[\[Phi]], r Cos[\[Theta]]}

Alternatively one may use the separable system of coordinates for the Laplacian at constant R.

CoordinateTransformData[{{"Toroidal", {R}} -> "Cartesian", "Euclidean", 3},
"Mapping"][{r, \[Theta], \[Phi]}]
ToroidalX[R_, r_, [Theta], [Phi]] = 
        {Cos[[Phi]] Sinh[r],   Sin[[Phi]] Sinh[r], Sin[[Theta]]}/
          (R/(Cosh[r] - Cos[[Theta]])
Manipulate[ParametricPlot3D[ 
map[R, r, [Theta], [Phi]], {[Phi], 0, 2 [Pi]}, {[Theta], 0,    2 [Pi] }, 
PlotStyle -> {Hue[0.7, 0.3], Opacity[0.2]}, 
  Mesh -> {12, 17},

  MeshStyle -> {{Red, Thickness[0.002]}, {Yellow, Thickness[0.005]}}], 
{{R, 3}, 0, 12}, {{r, 2}, -6, 20},
 {{map, ToroidalX}, {PolarX, ToroidalX}}, ControlPlacement -> Top]

kglr · Answer 6 · 2023-05-17T01:58:29.783

tube[t_] := ParametricPlot3D[{Sin[u], 1 - Cos[u], 0}/t, {u, -t Pi, t Pi}, 
 PlotRange -> {{-4, 4}, {-1, 4}, {-1, 1}}, 
 PlotStyle -> {FaceForm[Red, Yellow], Tube[.5]}, 
 Boxed -> False, 
 Axes -> False, SphericalRegion -> True, ImageSize -> 400]
Row[{tube[.001], tube[.3], tube[.7]}]

Manipulate[tube[t], {t, 10^-3, 1, .1}]

Animation at the top produced with

Export["tube.gif", Table[tube[t], {t, 10^-3, 1, 10^-2}]]

How to wrap a cylinder?

6 Answers6

Edit