2

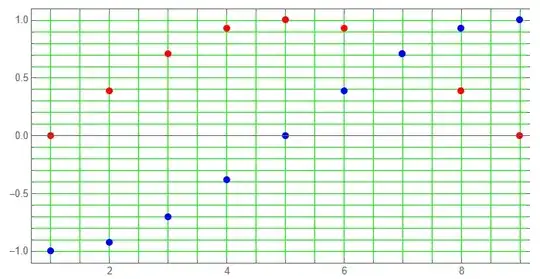
the problem I'm trying to solve is much more involved, that is I'm trying to get the Time Response for an Impulse Input for a loudspeaker starting from the pressure it generates over the frequency:enter image description here.
As you can see the Re part (Red) is symmetrical over the frequency, while the Im part (Blue) is anti-symmetrical, so, after the discretization and the InverseFourier, I would expect a Real result. None!
So I decided to make a simple example for your attention.

a = -(\[Pi]/2); b = \[Pi]/2; n = 9;
Rx = Range[a, b, (b - a)/(n - 1)];
T = Table[Cos[x] + I Sin[x], {x, Rx}];
G1 = ListPlot[Re[T], PlotRange -> {All, {-1.1, 1.1}}, PlotStyle -> Red];
G2 = ListPlot[Im[T], PlotRange -> {All, {-1.1, 1.1}}, PlotStyle -> Blue];
Show[{G1, G2}, GridLinesStyle -> Green]

enter image description here
Then I would expect that the

Z = InverseFourier[T, FourierParameters -> {1, -1}]

would give me real numbers. I get however

{0.558593 + 0. I, 0.197397 - 0.0718465 I, 0.107042 - 0.0898191 I, 0.0575418 - 0.0996653 I, 0.018928 - 0.107346 I, -0.020304 - 0.11515 I, -0.072473 - 0.125527 I, -0.17356 - 0.145634 I, -0.673165 - 0.245012 I}

What is the correct way to proceed?
Thanks

Teodoro Marinucci
  • 149
  • 7

1 Answers1

5

The convention in Fourier transforms is to put the negative part of the spectrum after the positive. As the function is periodic this is the same as your version. For some notes on Fourier see here.

Thus reworking your case

n1 = (n + 1)/2;
T1 = Join[T[[n1 ;; -1]], T[[1 ;; n1 - 1]]];
InverseFourier[T1]

giving

{1.67578 + 0. I, 2.1491 - 3.70074*10^-17 I, -0.679701 + 0. I, 
 0.434838 + 0. I, -0.350779 + 1.46701*10^-16 I, 
 0.327006 + 0. I, -0.345251 + 0. I, 
 0.419201 - 1.09694*10^-16 I, -0.630195 + 0. I}

As you can see all the imaginary parts are zero or numerical noise. You can remove this by using Chop. Note that for an even number of points you have to replace n1 with slightly different values.

Hugh
  • 16,387
  • 3
  • 31
  • 83