I have found that the Defer function, among others such as HoldForm or Inactive, seems to be the key to something I want to do, but I have been unable to figure out. If I calculate the value of a variable and then print it using Defer, it correctly shows me the name of the variable. Doing so in a matrix however simply prints out the name of the matrix rather than the names of the variables within that matrix. I understand why this is the case, but I am unable to figure out how to apply this Defer to the elements of the matrix rather than to the matrix as a whole.
As an example:
a1 = 42;
mat = {{a1, a2}, {b1, b2}};
Print[Defer[MatrixForm[mat]]]
Print["***"]
Print[MatrixForm[mat]]
This currently prints:
mat
***
42 a2
b1 b2
What I would like is:
a1 a2
b1 b2
***
42 a2
b1 b2
This is a minimal example. In my case, I have several matrices, which are not necessarily 2x2, for which I would like to show both the analytical and numerical versions.
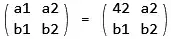


@is just the same as[...]so instead of writingfoo[4]you could, if you want, writef@4it saves one key stroke, that is all. If you are lazy, you'll find yourself using@more. – Nasser May 27 '23 at 22:40Identity@@ReleaseHold[mat]instead. – Somos May 30 '23 at 00:10First@ReleaseHold[mat]also. – Somos May 30 '23 at 02:28