Plotting Poincare section

Question

I am trying to plot the Poincare section. Is there any other method where I get results faster? I use Table to find points at an integer multiple of \phi, making NDSolve evaluate the solution for every integer m. Can I find the points at all integer m without evaluating NDSolve every time?

time = 10000; points = Flatten[Table[
Last[Reap[NDSolve[
   {34*Derivative[1][\[Theta]][t]*Cos[\[Psi][t]] + 
      34*Sin[\[Theta][t]]*Sin[\[Psi][t]]*
       Derivative[1][\[Phi]][t] + 
      4*Sin[2*\[Theta][t]]*Cos[\[Psi][t]]*
       Sin[2*\[Phi][t]] + Sin[\[Theta][t]]*
       Sin[\[Psi][t]]*(8*Cos[2*\[Phi][t]] + 
        17) == 0, 2*Sin[\[Psi][t]]*
      (13*Derivative[1][\[Theta]][t] + 
       3*Sin[2*\[Theta][t]]*Sin[2*\[Phi][t]]) == 
     Sin[\[Theta][t]]*Cos[\[Psi][t]]*
      (26*Derivative[1][\[Phi]][t] + 
       12*Cos[2*\[Phi][t]] + 13), 
    Cos[\[Theta][t]]*(10*Derivative[1][\[Phi]][
          t] + 4*Cos[2*\[Psi][t]]*
         Cos[2*\[Phi][t]] + 5) + 
      10*Derivative[1][\[Psi]][t] == 
     (Cos[2*\[Theta][t]] + 3)*Sin[2*\[Psi][t]]*
      Sin[2*\[Phi][t]], \[Phi][0] == 0, 
    \[Theta][0] == 15/10, \[Psi][0] == 15/10, 
    WhenEvent[Mod[\[Phi][t], m*Pi] == 0, 
     Sow[{ArcSin[Sin[\[Psi][t]]], \[Theta][t]}]]}, 
   {\[Theta][t], \[Phi][t], \[Psi][t]}, {t, 0, time}, 
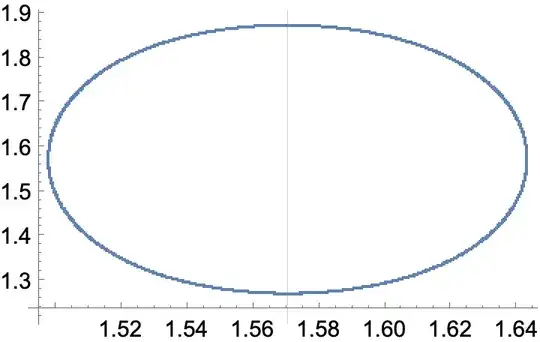
   MaxStepSize -> 1/50]]], {m, 1000}], 2]; plot = ListPlot[points]

It looks like you are computing the same quantity (i.e., Sin[theta], etc) at each iteration. Perhaps, use With[{st=Sin[theta],…},equations] to avoid superfluous numerical evaluations? — Craig Carter, May 31 '23 at 19:25
User @ plus username to notify people of a reply (e.g. @CraigCarter). I think what Craig is saying is that nothing really changes in the calls to NDSolve[] except the WhenEvent. So you could just do one call and find when Mod[\[Phi][t], m*Pi] == 0 afterwards. Alternatively, you can figure out all the data for m > 1 just from m == 1 by sampling every m-th reaped data point. — Michael E2, May 31 '23 at 20:15
Thanks @MichaelE2. What I was getting at is that your equations have many instances of computing the same quantity (such as Cos[phi[t]]), while each numerical evaluation is relatively fast, repeated calculations of the same quantity aren’t necessary. I’m just suggesting that you compute once and then use the result repeatedly at each iteration. Not an answer, but a suggestion for speeding things up. You could also Compile which will take care of the repeated calculations automatically. — Craig Carter, May 31 '23 at 21:24
Convert all trigonometrics to exponentials by TrigToTrue. Collect the exponentials via Cases and define them as products at each time t in terms of the simple exponentials a1=Exp[psi[t]] and 1/a1 =Exp[-psi[t] etc ]. The complicated trigonometric coefficients become simple rationals. Use NDSolve[ Print[t]; .... ] as the first command in the t-loop to see the performance. — Roland F, May 31 '23 at 21:37
Doesn't look to me it's catching all the mod points as written. With Mod[phi[t],Pi]==0, only catches one point but with Abs[Mod[phi(t),Pi]]<10^-3 it catches 77 which is more reasonable since Phi(t) drops from 0 to -400 in the interval of t. Suggest plotting solutions for one run and confirm getting all points. — josh, May 31 '23 at 21:58
Thanks @MichaelE2 and Craig Carter. I understand the logic behind the suggestion you have made, but I am unable to code and get the desired result. I will retry and code again and see if it works. — SanGu, Jun 01 '23 at 06:55
I am unable to get the result. Can someone help me with this? — SanGu, Jun 01 '23 at 07:30
@MichaelE2, can you help me with Craig's logic? I have understood the logic behind evaluating the NDSolve once (that is for m==1) and collecting data for every mth point, but I am unable to code and get the proper results. Thank you. — SanGu, Jun 02 '23 at 10:43

Michael E2 · Answer 1 · 2023-06-03T16:03:34.397

Here is my way, taking advantage of a zero-crossing routine by @davidC/@Mr.Wizard from this site to post-process the solution instead of using WhenEvent:

time = 10000;
ndsol = First@NDSolve[{
      {34*Derivative[1][\[Theta]][t]*Cos[\[Psi][t]] + 
         34*Sin[\[Theta][t]]*Sin[\[Psi][t]]*
          Derivative[1][\[Phi]][t] + 
         4*Sin[2*\[Theta][t]]*Cos[\[Psi][t]]*Sin[2*\[Phi][t]] + 
         Sin[\[Theta][t]]*Sin[\[Psi][t]]*(8*Cos[2*\[Phi][t]] + 17) == 
        0, 2*Sin[\[Psi][t]]*(13*Derivative[1][\[Theta]][t] + 
           3*Sin[2*\[Theta][t]]*Sin[2*\[Phi][t]]) == 
        Sin[\[Theta][t]]*
         Cos[\[Psi][t]]*(26*Derivative[1][\[Phi]][t] + 
           12*Cos[2*\[Phi][t]] + 13), 
       Cos[\[Theta][t]]*(10*Derivative[1][\[Phi]][t] + 
            4*Cos[2*\[Psi][t]]*Cos[2*\[Phi][t]] + 5) + 
         10*Derivative[1][\[Psi]][t] == (Cos[2*\[Theta][t]] + 3)*
         Sin[2*\[Psi][t]]*Sin[2*\[Phi][t]]}
      , {\[Phi][0] == 0, \[Theta][0] == 15/10, \[Psi][0] == 15/10}
      (*,WhenEvent[Mod[\[Phi][t],m*Pi]==0,Sow[{ArcSin[Sin[\[Psi][t]]],\[Theta][t]}]]*)
      }, {\[Theta], \[Phi], \[Psi]}, {t, 0, time}]; // AbsoluteTiming
(*  {0.129814, Null}  *)
(https://mathematica.stackexchange.com/a/10653)
(* Zero crossings in a list *)
davidZC2[l_] := 
 SparseArray[#]["AdjacencyLists"] & /. 
  SApos_ :> 
   With[{c = SApos[l]}, {c[[#]], c[[# + 1]]}[Transpose] &@
     SApos@Differences@Sign@l[[c]]]
piBrackets = 
   Sin[[Phi]["ValuesOnGrid"]] /. ndsol // davidZC2; // AbsoluteTiming
(*  {0.012167, Null}  *)
domain = Flatten[[Phi]["Domain"] /. ndsol]
range = MinMax[[Phi]["ValuesOnGrid"] /. ndsol]
(*
{0., 10000.}
{-4345.58, 0.}
*)
tvals = With[{tvals = Flatten[[Phi]["Grid"] /. ndsol]},
    t /. FindRoot[
        [Phi][t] == Round[[Phi][Mean@tvals[[#]]] /. ndsol, Pi] /. 
         ndsol
        , {t, Sequence @@ tvals[[#]]}, Method -> "Brent"] & /@ 
     piBrackets
    ]; // AbsoluteTiming
(*  {3.47713, Null}  *)
{[Psi][t], [Theta][t]} /. ndsol /. t -> tvals // Transpose // 
 ListPlot[#, GridLines -> {{Pi/2}, None}] &

I don't know why one wants to plot ArcSin[Sin[\[Psi][t]]] instead of \[Psi][t]. It just reflects the right half of the figure above across the grid line. However, if preferred, replace {\[Psi][t], \[Theta][t]} by {ArcSin[Sin[\[Psi][t]]], \[Theta][t]}.

I don't know why one would want to down-sample the return-times. There are only 1300+ times in tvals, so going up to m = 1000 only makes sense if time is greatly increased. However, if desired, one can down-sample with Span:

timesEvery[m_Integer?Positive] := tvals[[m ;; ;; m]];

The total time of execution is under four seconds.

josh · Answer 2 · 2023-06-03T20:50:49.080

3

Edit: Changed WhenEvent to Sow $t$ when $\sin(\phi(t))=0$ as per Michael's suggestion

Here's my solution using WhenEvent[Sin[\[Phi][t]] == 0, Sow[t]] as per Michael's suggestion. Takes about 0.3 seconds at 4.0 GHz.

    AbsoluteTiming[
 solF = Reap[
    NDSolveValue[{34*Derivative[1][\[Theta]][t]*Cos[\[Psi][t]] + 
        34*Sin[\[Theta][t]]*Sin[\[Psi][t]]*Derivative[1][\[Phi]][t] + 
        4*Sin[2*\[Theta][t]]*Cos[\[Psi][t]]*Sin[2*\[Phi][t]] + 
        Sin[\[Theta][t]]*Sin[\[Psi][t]]*(8*Cos[2*\[Phi][t]] + 17) == 
       0, 2*Sin[\[Psi][t]]*(13*Derivative[1][\[Theta]][t] + 
          3*Sin[2*\[Theta][t]]*Sin[2*\[Phi][t]]) == 
       Sin[\[Theta][t]]*
        Cos[\[Psi][t]]*(26*Derivative[1][\[Phi]][t] + 
          12*Cos[2*\[Phi][t]] + 13), 
      Cos[\[Theta][t]]*(10*Derivative[1][\[Phi]][t] + 
           4*Cos[2*\[Psi][t]]*Cos[2*\[Phi][t]] + 5) + 
        10*Derivative[1][\[Psi]][t] == (Cos[2*\[Theta][t]] + 3)*
        Sin[2*\[Psi][t]]*Sin[2*\[Phi][t]], \[Phi][0] == 
       0, \[Theta][0] == 15/10, \[Psi][0] == 15/10, 
      WhenEvent[Sin[\[Phi][t]] == 0, Sow[t]]}, {\[Theta][t], \[Phi][
       t], \[Psi][t]}, {t, 0, 10000}]];
 ]

Then post-processing the points as requested:

    theta[t_] = solF[[1, 1]];
phi[t_] = solF[[1, 2]];
psi[t_] = solF[[1, 3]];
Plot[phi[t], {t, 0, 10000}]
dataPoints = {ArcSin[Sin[psi[#]]], theta[#]} & /@ Flatten[solF[[2]]];
ListPlot[dataPoints, AspectRatio -> 1, 
 PlotLabel -> 
  Style["ArcSin[Sin[\[Psi](t)]] vs. \[Theta](t)", 16, Bold, Black]]

edited Jun 03 '23 at 20:50

answered Jun 02 '23 at 19:01

josh

2,352
4
17

1

Assuming the OP will see this comment, I suspect the OP saw Mod[t, Δt] in the docs for WhenEvent and assumed that Mod[φ[t], Δt] would work. But Mod[t, Δt] is a special case for periodic sampling with special handling by NDSolve. So Mod[φ[t], Pi] == 0 receives the generic treatment of looking for zero-crossings, which there should be none, barring round-off error. One might think that Mod[φ[t], Pi, Pi/2] == 0 might work, since there is a sign change at every multiple of Pi; however, there is also a sign change every multiple of Pi/2. This then gives too many times, and... – Michael E2 Jun 02 '23 at 19:20
2

...the root-finding complains since Mod[] is discontinuous. My suggestion is to use Sin[φ[t]] == 0 and omit MaxStepSize. Then things are quite fast, as they should be. This should not be a computationally hard problem. – Michael E2 Jun 02 '23 at 19:20
@Michael E2: Brilliant. Takes 0.3 seconds that way! – josh Jun 02 '23 at 19:30
1

@ josh, Feel free to incorporate Sin[φ[t]] == 0 into your code. Or at least upvote my comment. I feel the difference between Mod[φ[t], Pi] == 0, Mod[φ[t], Pi, -Pi/2] == 0, and Sin[φ[t]] == 0 should be a highlight of this Q&A. – Michael E2 Jun 03 '23 at 16:08
@Michael E2: Ok, updated code as per your request. – josh Jun 03 '23 at 20:51

score 0 · Answer 3 · answered Jun 02 '23 at 17:04

0

Here is one of the methods that I have used to increase the speed of the computation.

whenevent = Table[With[{m = m}, WhenEvent[Mod[\[Phi][t], m*Pi] == 
         0, Sow[{ArcSin[Sin[\[Psi][t]]], \[Theta][t]}]]], {m,2000}];time = 10000; points = Flatten[
 Table[Last[Reap[NDSolve[
         {4*Cos[\[Psi][t]]*Sin[2*\[Theta][t]]*Sin[2*\[Phi][t]] + 
               (17 + 8*Cos[2*\[Phi][t]])*Sin[\[Theta][t]]*
      Sin[\[Psi][t]] + 
               34*Cos[\[Psi][t]]*Derivative[1][\[Theta]][t] +
 34*Sin[\[Theta][t]]*Sin[\[Psi][t]]*Derivative[1][\[Phi]][t] == 
0, 


2Sin[[Psi][t]](3Sin[2[Theta][t]]Sin[2[Phi][t]] + 
                  13Derivative[1][[Theta]][t]) == 
    Cos[[Psi][t]]Sin[[Theta][t]]*
               (13 + 12Cos[2[Phi][t]] + 
       26*Derivative[1][[Phi]][t]),
Cos[[Theta][t]](5 + 4Cos[2*[Phi][t]]Cos[2[Psi][t]] + 
                    10Derivative[1][[Phi]][t]) + 
     10Derivative[1][[Psi]][
                   t] == (3 + Cos[2*[Theta][t]])Sin[2[Phi][t]]*
               Sin[2*[Psi][t]], [Phi][0] == 0, [Theta][0] == 
    15/10, 
           [Psi][0] == 15/10, 
   whenevent}, {[Theta], [Phi], [Psi]}, 
         {t, 0, time}, MaxStepSize -> 1/50]]], {m, 1000}], 1];plot = ListPlot[points]

answered Jun 02 '23 at 17:04

SanGu

41
5

How long does it take? – Michael E2 Jun 02 '23 at 17:34
@user1163335: Can you just solve the DEs without Table, Last or WhenEvent? Just NDSolve (preferably NDSolveValue) the DEs and then just plot $\theta(t)$, $\psi(t)$, and $\phi(t)$? – josh Jun 02 '23 at 18:03
As written, looks to me $m$ is unnecessary: simply run the code once sowing $t$ WhenEvent[Phi(t) mod pi]<small value and plot the results. May have to adjust integration parameters though. Haven't looked at it in detail though. – josh Jun 02 '23 at 18:20
Thank you @MichaelE2, your logic of using Sin[\phi] is very brillient it worked super fast. – SanGu Jun 03 '23 at 15:59
Thank you everyone, I get to learn so many new ways of solving this particular problem in mathematica. – SanGu Jun 03 '23 at 16:01

Plotting Poincare section

3 Answers3