Let's try to do 10 ways.
Courtesy of @cvgmt in the comments under the OP
{list1, list2} // Transpose
{list1, list2} // Thread
My original answer
Inner[List, list1, list2, List]
ArrayReduce[Dot, {list1, list2}, 1]
ArrayReshape[Riffle[list1, list2], {Length@list1, 2}]
MapThread[List, {list1, list2}]
Table[{list1[[i]], list2[[i]]}, {i, 1, Length@list1}]
Another great recommendation by @cvgmt as a comment under this answer
Outer[List, list1, list2] // Diagonal
@Nasser's suggested solution
MapThread[{#1, #2} &, {list1, list2}]
@Michael E2 used J. M.'s function in the following way
columnAttach[{1, 2, 3}, {a, b, c}]
All of the above give
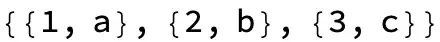
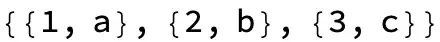
list1 = {1, 2, 3}; list2 = {a, b, c}; {list1, list2} // TransposeorThread– cvgmt Jun 02 '23 at 00:25columnAttach[{1, 2, 3}, {a, b, c}]from here – Michael E2 Jun 02 '23 at 01:11List Manipulation– Bob Hanlon Jun 02 '23 at 02:29