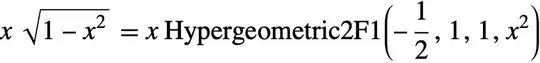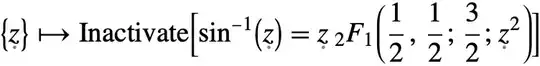5

For example, I have a function

f[x_] = x*Sqrt[1 - x^2] + ArcSin[x]

Is there a way to convert such functions to (a sum of) hypergeometric functions?

In this case $f$ is an antiderivative of $2\sqrt{1-x^2}$, so it's possible. Funnily, for the Meijer G function there is command MeijerGReduce[], but I didn't manage to find something like that for hypergeometric functions.

Andrew
  • 2,513
  • 17
  • 15

2 Answers2

7
Clear["Global`*"]

f[x_] = x*Sqrt[1 - x^2] + ArcSin[x];

For the first term of f[x],

coef1[n_] = Assuming[Mod[-1 + n, 2] == 0 && n >= 1,
  SeriesCoefficient[x*Sqrt[1 - x^2], {x, 0, n}] // FullSimplify]

(* -(Gamma[-1 + n/2]/(2 Sqrt[π] Gamma[(1 + n)/2])) *)

Verifying,

Sum[coef1[2 n + 1] x^(2 n + 1), {n, 0, Infinity}]

(* x Sqrt[1 - x^2] *)


(coef1[2 n + 1] // Simplify) /. Gamma[n + a_] :> Pochhammer[a, n]*Gamma[a]


(* Pochhammer[-(1/2), n]/Pochhammer[1, n] *)

Consequently,

(x*Sqrt[1 - x^2] == x*Inactive[Hypergeometric2F1][-1/2, 1, 1, x^2]) //
 TraditionalForm

enter image description here

% // Activate

(* True *)

For the second term of f[x],

Entity["MathematicalFunction", "ArcSin"][
   "HypergeometricRepresentations"][[1]] // TraditionalForm

enter image description here

%[x] // Activate

(* True *)

Then

(f[x] == x (Inactive[Hypergeometric2F1][-1/2, 1, 1, x^2] +
      Inactive[Hypergeometric2F1][1/2, 1/2, 3/2, x^2])) //
 TraditionalForm

enter image description here

% // Activate // Simplify

(* True *)
Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
5

I used Roman's method (under derivation) from this post.

f[x_] = x*Sqrt[1 - x^2] + ArcSin[x]

Series[f[x], {x, 0, 10}]


(* x - x^3/3 - x^5/20...*)

note that all terms are of the form $x^{1+2n}$ with integer . We can get the series coefficients and find a fitting function:

Table[{n, SeriesCoefficient[f[x], {x, 0, 2 n + 1}]}, {n, 0, 10}]
(*{{0, 2}, {1, -(1/3)}, {2, -(1/20)}, {3, -(1/56)}, {4, -(5/
   576)}, {5, -(7/1408)}, {6, -(21/6656)}, {7, -(11/5120)}, {8, -(429/
   278528)}, {9, -(715/622592)}, {10, -(2431/2752512)}}*)

FindSequenceFunction[%, n]


((2 Pochhammer[-(1/2), n])/((-1 + 2 (1 + n)) Pochhammer[1, n]))

Then, note that:

Sum[(2 Pochhammer[a, n])/(Pochhammer[1, n] + 2 n Pochhammer[1, n])* 
  x^(1 + 2 n), {n, 0, \[Infinity]}]
(*2 x Hypergeometric2F1[1/2, a, 3/2, x^2]*)

so with a = -1/2 in our case we get x*Sqrt[1 - x^2] + ArcSin[x] = 2 x Hypergeometric2F1[1/2, -1/2, 3/2, x^2]

ydd
  • 3,673
  • 1
  • 5
  • 17