I have a list of coefs of the form $1,1/4,1/9,1/16,\ldots,1/d^2$ sampled with relative sampling frequencies $1,1/4,1/9,1/16,\ldots,1/d^2$.
How do I find a nice continuous density whose CDF closely matches the CDF of the distribution above?
The code below finds a close match to a simpler distribution, which uses sampling frequencies $1,1,1,1,\ldots$ instead of $1,1/4,1/9,1/16,\ldots$, I was looking for an elegant way to extend this to the distribution above
ClearAll["Global`*"];
d = 20; p = 2; $Assumptions = {0 < x < 1, 0 < y < 1};
coefs = Table[i^-p, {i, 1, d}];
{min, max} = MinMax[coefs];
dist = EmpiricalDistribution[coefs];
pdf = y^-(1 + 1/p) Boole[min <= y <= max];
pdf = pdf/Integrate[pdf, {y, 0, 1}];
Print["continuous pdf: ", pdf];
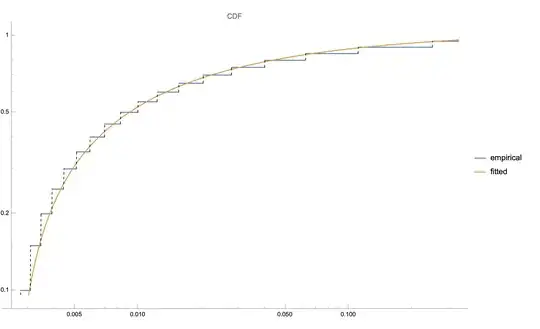
fittedCDF = Integrate[pdf, {y, 0, x}];
LogLogPlot[{CDF[dist, x], fittedCDF}, {x, min, 1/3},
ExclusionsStyle -> Dashed, PlotLegends -> {"empirical", "fitted"},
PlotLabel -> "CDF"]
For a more general setting, related question by Vitaly Kaurov is here.
Motivation: moment generating function of this density gives the loss curve observed when minizing $x_1^2+\frac{1}{4}x_2^2+\frac{1}{9}x_3^2+\ldots$ from a random starting point, see this community post
Summarizing briefly
loss after $t$ steps of GD minimizing $h_1 x_1^2 + h_2 x_2^2 \ldots + h_d x_d^2$ using step size $1$ and starting with $\mathbf{x0}$ is $$\sum_i h_i(1-h_i)^{2t} \mathbf{x0}_i^2$$
using a certain kind of random initial point $\mathbf{x0}$ we get the following in expectation
$$\sum_i h_i(1-h_i)^{2t}$$
- approximating $(1-h_i)$ with $\exp(-h_i)$ we get $$\sum_i h_i \exp(-2 t h_i)$$
This approximation is valid when $\max_i h_i < 1$ and the problem is "high-dimensional", it has a high effective rank R defined in Bartlett paper
- Now writing the previous sum in terms of expectation we get the following for some constant $c$ and expectation taken over empirical density of $h$
$$c E_h[h \exp(-2t h)]$$
Now modify the empirical density of $h$ by sampling each $h_i$ with relative frequency proportional to $h_i$, call this density $\hat{h}$. We can write our loss as expectation below $$c E_\hat{h}[\exp(-2t h)]$$
Observe the close relation of formula above to the moment generating function of $\hat{h}$

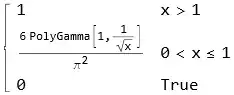


BetaDistribution[1/9 (21 - 2 \[Pi]^2), (315 - 51 \[Pi]^2 + 2 \[Pi]^4)/(9 \[Pi]^2)]. And it seems you have a random variable rather than a "process". – JimB Jun 22 '23 at 04:53EmpiricalDistribution[coefs]but stuck finding one forEmpiricalDistribution[coefs->coefs]. I care about close match between CDFs rather than moments – Yaroslav Bulatov Jun 22 '23 at 16:31