Given the u or v of the analytic function f(z), find f(z):
z=x+I y,
f[z]=u[x,y]+I v[x,y]
Given $v=\left[-x+\left(x^2+y^2\right)^{1 / 2}\right]^{1 / 2}, f(0)=0$
Then find f[z].
First, I get u[x,y] by Total derivative method.
(Cite from https://mathematica.stackexchange.com/a/79074/69835)
Clear["Global`*"];
exactQ[{P_, Q_}, {x_, y_}] := D[P, y] == D[Q, x] // Simplify;
exactQ[{P_, Q_, R_}, vars_] :=
Curl[{P, Q, R}, vars] == {0, 0, 0} // Simplify;
exactSolve[vf_, vars_] /; exactQ[vf, vars] :=
Fold[#1 + Integrate[#2[[1]] - D[#1, #2[[2]]], #2[[2]]] &, 0,
Transpose[{vf, vars}]]
v[x_, y_] := (-x + (x^2 + y^2)^(1/2))^(1/2)
dtu[x_, y_] := {D[v[x, y], y], -D[v[x, y], x]}
u[x, y] = exactSolve[dtu[x, y], {x, y}]
(* $\frac{y}{\sqrt{-x+\sqrt{\mathrm{x}^2+\mathrm{y}^2}}}$ *)
Then I tried to find f[z], but the result was not completely simplified. I don't know what caused it and how to modify the code. The correct answer in the textbook is $f(z)=\sqrt{2 z}$.
ClearAll["Global`*"]
u[x, y] = y/Sqrt[-x + Sqrt[x^2 + y^2]];
v[x, y] = (-x + (x^2 + y^2)^(1/2))^(1/2);
f[x, y] = (u[x, y] + c) + I v[x, y] // Simplify
eq = Simplify[f[x, y], {x + I*y == z}] /. z -> 0
sol = Solve[eq == 0, c]
f[x, y] = f[x, y] /. sol[[1]]
expr = Simplify[f[x, y], {x + I*y == z}]
(* $-\frac{{\mathbb{i} z}}{\sqrt{-x+\sqrt{x^2+y^2}}}$ *)
EDIT
ClearAll["Global`*"]
u[x, y] = y/Sqrt[-x + Sqrt[x^2 + y^2]];
v[x, y] = (-x + (x^2 + y^2)^(1/2))^(1/2);
f[x, y] = u[x, y] + c + I v[x, y];
eq = Simplify[f[x, y], {x + I*y == z}] /. z -> 0;
sol = Solve[eq == 0, c];
f[x, y] = f[x, y] /. sol[[1]]
f[z_] :=
FullSimplify[
f[x, y] /. {x -> (z + Conjugate[z])/2,
y -> (z - Conjugate[z])/(2 I)}, Element[x | y, Reals]];
f[z]
(* -((I z)/Sqrt[Abs[z] - Re[z]]) *)
But the result -((I z)/Sqrt[Abs[z] - Re[z]]) cannot be simplified to the textbook result Sqrt[2 z]. I did not detect any obvious errors in my code, and it obtained correct results when used on other complex functions. I don't know where the problem is.
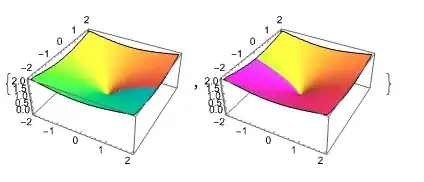
u[x,0]+I v[x,0]– Lacia Jul 02 '23 at 10:10-((I z)/Sqrt[Abs[z] - Re[z]])toSqrt[2 z]?" This is not true: compare the results ofComplexPlot[-((I z)/Sqrt[Abs[z] - Re[z]]), {z, -2 - 2*I, 2 + 2*I}]andComplexPlot[Sqrt[2 z], {z, -2 - 2*I, 2 + 2*I}]. – user64494 Jul 03 '23 at 05:17FullSimplify. – user64494 Jul 03 '23 at 10:15