Find the zero crossing in data

Question

I have the following list. l = Table[Sin[i], {i, -4 Pi, 4 Pi}] // N which gives me the following data, {0., 0.8414709848078965, 0.9092974268256817, 0.1411200080598672, -0.7568024953079283, -0.9589242746631385, -0.2794154981989259, 0.6569865987187891, 0.9893582466233818, 0.4121184852417566, -0.5440211108893698, -0.9999902065507035, -0.5365729180004349, 0.4201670368266409, 0.9906073556948704, 0.6502878401571168 -0.2879033166650653, -0.9613974918795568, -0.7509872467716762, 0.1498772096629523, 0.9129452507276277, 0.836655638536056, -0.008851309290403876, -0.8462204041751706, -0.9055783620066239, -0.132351750097773} 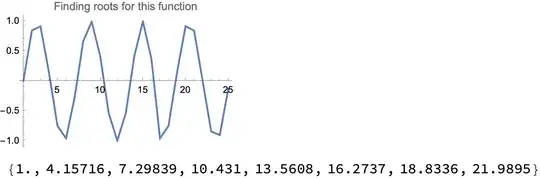Then I plotted the data with ListLinePlot[l]. The plot is the following picture

Now, if I want to know the value of each zero crossing with the x-axis, can I interpolate over data and use the FindRoot function? I tried this method but I was not successful.

I appreciate it if you could help me.

score 7 · Accepted Answer · answered Jul 03 '23 at 08:09

7

$Version
"13.3.0 for Microsoft Windows (64-bit) (June 3, 2023)"

l = Table[Sin[i], {i, -4 Pi, 4 Pi}];
data = l // N;
plot = ListPlot[data, Joined -> True, MeshFunctions -> {#2 &}, 
  Mesh -> {{0}}, MeshStyle -> Red]
Cases[plot, Point[{root_, 0.}] :> root, -1]

answered Jul 03 '23 at 08:09

cvgmt

72,231
4
75
133

Thanks! Is it possible to apply this method to any periodic data to find the zero-crossings? – Lohrasb Jul 03 '23 at 08:12
Unfortunately, the zero values are not printed since I try your idea! – Lohrasb Jul 03 '23 at 08:34
@Lohrasb We need to use version 13.3. https://www.wolfram.com/mathematica/quick-revision-history/ – cvgmt Jul 03 '23 at 08:35
It works perfectly with the new version. Thanks a lot! – Lohrasb Jul 03 '23 at 11:23
With the code Cases[plot, {root_, 0.} :> root, -1] with version 10.2 and even earlier it will work – Sigis K Jul 12 '23 at 19:40

chris · Answer 2 · 2023-07-04T08:27:25.303

You could use FindRoot as follows

l = Table[{i, Sin[i]}, {i, -4 Pi, 4 Pi, Pi/4}] // N;
ff = Interpolation[l, InterpolationOrder -> 3, 
   PeriodicInterpolation -> True];

Then

{ListLinePlot[l,InterpolationOrder -> 3], 
  ListPlot[
   Table[{x /. 
       FindRoot[ff[x] == 0, {x, RandomChoice[First /@ l, 1]}] // 
      First, 0},
    {100}], PlotStyle -> Red]} // Show

See FindAllCrossing2D for a generalisation in higher dimensions.

To get the values themselves just try

Table[x /. FindRoot[ff[x] == 0, {x, RandomChoice[First /@ l, 1]}] // 
   First, {100}]/Pi // Chop // Union // Rationalize // (# Pi) &

Note that thanks to the periodicity it finds other points beyond the range considered :-)

Thanks, but how can I know what are the values? – Lohrasb Jul 03 '23 at 08:24 — Lohrasb, Jul 03 '23 at 08:24

score 1 · Answer 3 · answered Jul 03 '23 at 23:32

I guess we should acknowledge recycling ideas. For my contribution to this Q&A, I'll cite Jen's 2012 findAllRoots[] from Find all roots of an interpolating function (solution to a differential equation), which was written to find all roots of an interpolating function, essentially the very problem in this question.

findAllRoots[
 Interpolation[l, x, InterpolationOrder -> 1], {x, 0.999999, 
  Length[l]}, "ShowPlot" -> True]

Or, alternatively:

findAllRoots[
 Interpolation[l, x], {x, 1 - 2^32 $MachineEpsilon, Length[l]}, 
 "ShowPlot" -> True]

It is remarkable that such a basic problem as the OP's is still not addressed by a standard Mathematica solver. Jens' answer is over ten year old! NSolve will use an internal plot-based solver on some equations, using a method similar to @cvgmt's and seen many times on this site. NSolve then polishes the roots with FindRoot, since the values from plotting are close but not usually highly accurate. This step should be considered necessary if interpolating with a smooth spline as in @Chris's answer. For linear interpolation, such as ListPlot does in @cvgmt's answer, the plot probably gives an accurate estimate of the roots of the linear interpolant. Linear interpolation is the principal source of error in that method.

P.S. Feel free to vote to close as a duplicate. Given the question, "can I interpolate over data and use the FindRoot function?", this seems the same as the one I linked.

Find the zero crossing in data

3 Answers3