Eliminate artifacts in a region region defined by `RegionDifference`

Question

Consider the following region:

Vol2 = Parallelepiped[{-4.8, -4, 
    15}, {{9.6, 0, 0}, {0, 8, 0}, {0, 0, 4}}];
Vol1 = Parallelepiped[{-0.3, -0.25, 
    15}, {{0.6, 0, 0}, {0, 0.5, 0}, {0, 0, 4}}];
Vol = RegionDifference[Vol2, Vol1];

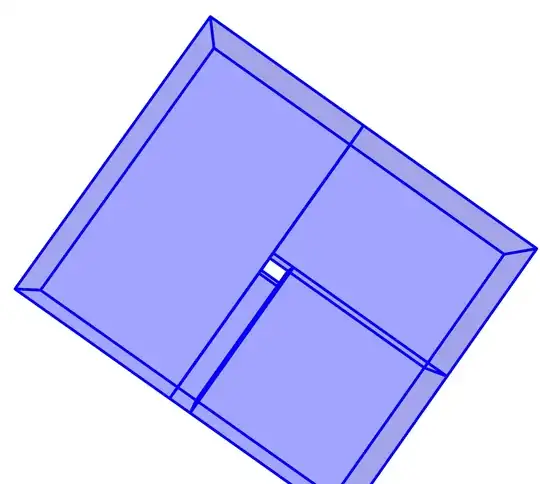
Its visualization is imperfect:

Region[Style[Vol, Blue, Opacity[0.2], EdgeForm[{Thick, Blue}]]]

Could you please tell me how to get a smooth visualization?

P.S. The method from the question does not work:

Vol // BoundaryDiscretizeRegion // Region`Mesh`MergeCells

BoundaryMeshRegion::bsuncl: The boundary surface is not closed because the edges Line[{{11,14},{21,24},{10,1},{14,7},{24,23},{19,17},{20,19},{13,10},{7,4},{23,22},<<6>>}] only come from a single face.

Missing the upper and lower surfaces. reg = RegionBoundary[Vol] // DiscretizeRegion; Graphics3D[{FaceForm[ Directive[Opacity[.2], Blue]], EdgeForm[Thick], reg // Region\Mesh`MergeCells}, Boxed -> False]` — cvgmt, Jul 06 '23 at 01:05

score 2 · Accepted Answer · answered Jul 06 '23 at 04:32

Three ways to get a visualization without internal edge lines:

DiscretizeRegion[vol, MaxCellMeasure -> "Volume" -> 1]

Graphics3D[{EdgeForm[None], vol}, Boxed -> False]

And this can have edge lines at the corners, thought it's a bit roundabout and uses an internal function:

polyContainsQ // ClearAll;
polyContainsQ[poly_Polygon, point_List] := 
  RegionDistance[poly, point] < 1.*^-6; (* tolerance *)
polyContainsQ[poly1_Polygon, poly2_Polygon] := 
  AllTrue[First@poly2, polyContainsQ[poly1, #] &];
polyContainsQ[poly1_Polygon, polys2 : {__Polygon}] := 
  AllTrue[polys2, polyContainsQ[poly1, #] &];
NDSolveFEMToBoundaryMesh[vol, "MeshOrder" -> 1] // MeshRegion[#] & //
    Show // Normal;
% /. polys : {__Polygon} :> 
    GatherBy[polys, #[[1, 1]] Boole@MapThread[Equal, First@#] &] /.
  polys : {__Polygon} :>
   With[{mesh = GraphicsMeshMeshObject[{polys}]},
    With[{boundaries = 
       Polygon /@ mesh@"Coordinates"[Most /@ mesh@"BoundaryVertices"]},
     Replace[boundaries,
      {b : {_Polygon} :> First@b,
       b : {__Polygon} :> Catch[
         Do[
          If[polyContainsQ[b[[i]], Drop[b, {i}]],
           Throw[Polygon[First@b[[i]] -> First /@ Drop[b, {i}]]]
           ],
          {i, Length@b}
          ]
         ]}
      ]
     ]] /. _EdgeForm -> Nothing

score 2 · Answer 2 · answered Jul 06 '23 at 16:12

A little complicates but using method in: Extract 2D quad mesh from 3D hexahedral mesh

bmesh = BoundaryMeshRegion[Vol];
enormal = Chop[Region`Mesh`MeshCellNormals[bmesh, 2]];
mg = MeshConnectivityGraph[bmesh, {1, 2}];
edges = VertexList[mg, {1, _}];
adj = (AdjacencyList[mg, #] & /@ edges)[[All, All, 2]];
corneredges = Pick[edges, Dot @@ enormal[[#]] & /@ adj, x_ /; x < 1];
edges = MeshPrimitives[bmesh, corneredges];
Graphics3D[{Style[Vol, Blue, Opacity[0.2], EdgeForm[None]], {Thick, 
   Blue, edges}}, Boxed -> False]

Eliminate artifacts in a region region defined by `RegionDifference`

2 Answers2