A complicated integral

Question

I'm trying to do this complicated integral:

And my code is as follows:

f[k_] := 
 k^3 (ln[1 + 2.34 k]/(2.34 k))^2 (1 + 
    3.89 k + (16.1 k)^2 + (5.46 k)^3 + (6.71 k)^4)^-0.5 (3 Sin[k*R]/(k*R)^3 - 3 Cos[k*R]/(k*R)^2)^2
NIntegrate[f[k], {k, 0, Infinity}, Assumptions -> {R > 0}]

But I can't get an answer and what I would like to do in the end is to draw a figure about F(R).

Could you please help me with that? Thanks in advance!

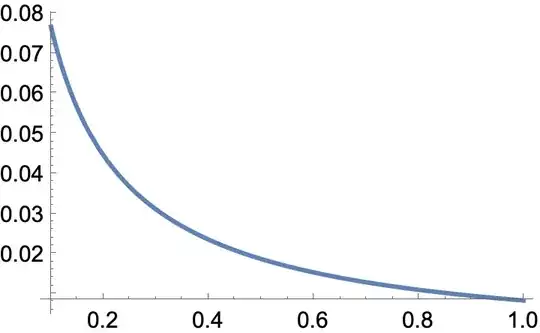
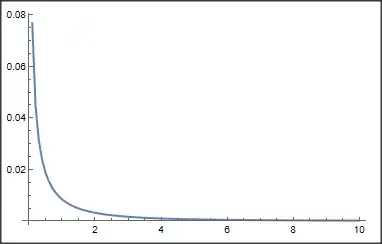
(1) Some basic syntax: Sin not sin, Cos not cos, etc. (2) Decimal points in numbers represent approximate floating point numbers. It's best to use exact numbers (e.g. rational fractions) in exact solvers like Integrate. (Round-off error sometimes messes up exact computations.) (3) Some integrals are too hard for Mathematica or any other system to solve symbolically. Would a numerical approach work for you? It might be an easier to plot a graph. — Michael E2, Jul 14 '23 at 17:49
Some advice for people learning Mma: https://mathematica.stackexchange.com/a/18395/4999 — Michael E2, Jul 14 '23 at 17:49
Forgot this tip: You can format inline code and code blocks by selecting the code and clicking the {} button above the edit window. The edit window help button ? is useful for learning how to format your questions and answers. You may also find the meta Q&A, How to copy code from Mathematica so it looks good on this site, helpful — Michael E2, Jul 14 '23 at 17:51
Thank you so much for your advice. I try to use NIntegrate and replace every floating point number into integers but still can not get a result, could you please help me with that? — Runyu Liao, Jul 14 '23 at 18:03

score 2 · Answer 1 · answered Jul 14 '23 at 18:34

Another answer to What are the most common pitfalls awaiting new users? explains the use of _?NumericQ and has links to similar Q&A as this one.

f[k_, R_] := (* tip: avoid initial capitals (use r not R) *)
 k^3 (Log[1 + 2.34 k]/(2.34 k))^2 (1 + 
     3.89 k + (16.1 k)^2 + (5.46 k)^3 + (6.71 k)^4)^-0.5 (3 Sin[
        k*R]/(k*R)^3 - 3 Cos[k*R]/(k*R)^2)^2;
ff[r_?NumericQ] := NIntegrate[f[k, r], {k, 0, Infinity}];
Plot[ff[R], {R, 1/10, 1}]

score 1 · Answer 2 · answered Jul 14 '23 at 18:34

The logarithm is written "Log". Further, "NIntegrate" can only do numerical integrals. Therefore, you must replace "R" by a number ("DSolve" take a long time.):

f[k_] := 
 k^3 (Log[1 + 2.34 k]/(2.34 k))^2 (1 + 
     3.89 k + (16.1 k)^2 + (5.46 k)^3 + (6.71 k)^4)^-0.5 (3 Sin[
        k*R]/(k*R)^3 - 3 Cos[k*R]/(k*R)^2)^2
d = Table[{R, NIntegrate[f[k], {k, 0, Infinity}]}, {R, 0.1, 10, 
    0.1}];
ListLinePlot[d, PlotRange -> All]

A complicated integral

2 Answers2