6

I have been grappling with a physics calculation pertaining to thin film optics. I have been endeavouring to use transfer matrix calculations to determine optical reflectance. Attached below is the code I authored:

(*Angle of 30° for p polarisation*)
ClearAll["Global`*"]
θ1 = 30°;
θ2 = ArcSin[(n1*Sin[θ1])/n2];
δ1 = π/2*Cos[θ1];
δ2 = π/2*Cos[θ2];
γ1 = n1/Cos[θ1];
γ2 = n2/Cos[θ2];

matrixA = {{Cos[δ1],(ISin[δ1])/γ1},{Iγ1Sin[δ1],Cos[δ1]}};
matrixB = {{Cos[δ2],(ISin[δ2])/γ2},{Iγ2Sin[δ2],Cos[δ2]}};
matrixC = matrixA . matrixB;


Text["Here is Matrix BC:"];
matrixD = matrixC . {{1},{n-I*k}};


β = matrixD[[1,1]];
α = matrixD[[2,1]];
Y = α/β;


Text["Here is r - known as reflection coefficient"];
r = (1-Y)/(1+Y);
n = 300;
k = 300;
(This section calculates the reflectance)
R = FullSimplify[r * Conjugate[r], Assumptions-> n1>0 && n2>0];
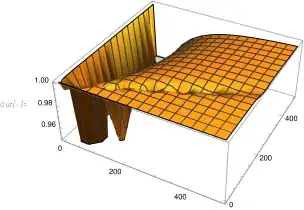
Plot3D[R, {n1,0.01,500},{n2,0.01,500}]
Text["This is The minimum"]
NMinimize[{R, n1>0 && n2>0},{n1,n2}]

In the key phenomenon of interest, an electromagnetic wave beam hits a two-layer coating on a metal substrate.

  • n1, refractive index of the first layer.
  • n2, refractive index of the second layer.
  • n-ik, complex index of the metal substarate.

Using transfer matrices, I want to determine the reflectance of the entire system. However, Mathematica returns complex values for R which, I have confirmed manually, should be a purely real number. Mathematica's results, conversely, still contains an imaginary part, so numerical minimization fails:

"The function value 0.993195 - 2.77556*10^-17 I is not a real number at {n1, n2} = {1.91862,1.66351}."

Addio, even if I define R to the result of my manual derivation, minimization of that expression produces a negative value for R, which is not physically meaningful.

Is there an alternative method for encoding the algorithm so Mathematica performs the computations successfully?

MarcoB
  • 67,153
  • 18
  • 91
  • 189
Hooman Puyandeh
  • 65
  • 4
  • 6
    I suggest to use Chop[] at appropriate places to remove numerical noise including irrelevant small imaginary parts, which unfortunately sometimes crop up in numerical calculations. Before claiming that Mathematica cannot do Complex Conjugation properly I would suggest to start to think properly, It always appears to be a good first assumption that the problem sits actually in front of the screen. – Michael Weyrauch Jul 16 '23 at 17:08
  • 3
    If you're working with numeric values, you can also write a simple version of Conjugate yourself using a pattern like Complex[x_,y_] :> Complex[x,-y] as a test. If applying this rule to your data gives the same results, it's unlikely to be the Conjugate function. –  Jul 16 '23 at 17:20
  • 3
    The previous comments are good and what one typically does to avoid round-off errors that otherwise results in numbers with a very small imaginary component. Another way that seems to work here is rewriting R as R = Re[r]^2 + Im[r]^2;. – JimB Jul 16 '23 at 18:59

1 Answers1

6

Following the suggestion of @JimB, but using Abs[r]^2 instead, I get the following. (I only put the last few lines with the change and the code affected by the change. Everything else is the same as what you posted.)

(*This section calculates the reflectance*)
R = FullSimplify[(*r*Conjugate[r]*)Abs[r]^2, 
   Assumptions -> n1 > 0 && n2 > 0];
Plot3D[R, {n1, 0.01, 500}, {n2, 0.01, 500}]
Text["This is The minimum"]
NMinimize[{R, n1 > 0 && n2 > 0}, {n1, n2}]

Plot3D

Text["This is The minimum"]

{2.68381*10^-19, {n1 -> 0.174611, n2 -> 5.04473}}

Small, but positive.