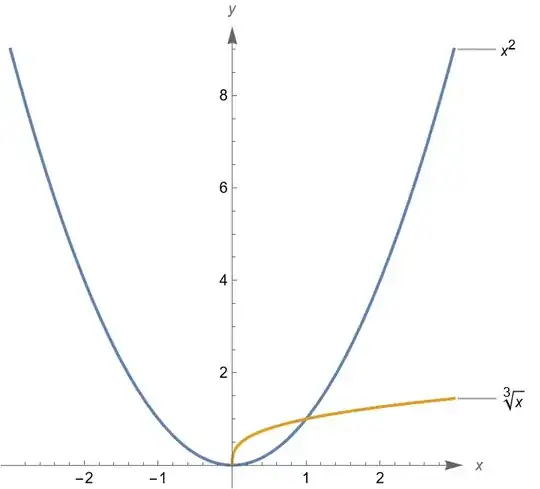
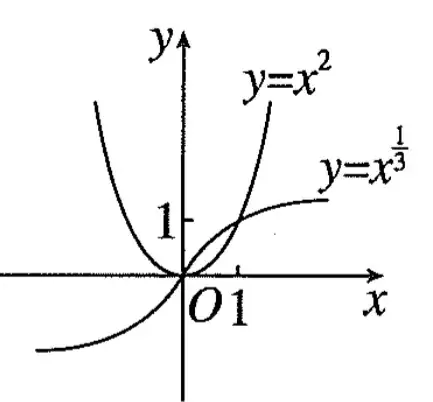
Solve this inequality
In[41]:= Reduce[x^2 > x^(1/3), x, Reals]
Out[41]= x > 1
Missing a solution as
x<0
There was also an error in drawing images of two functions within the same coordinate system
Plot[{x^2, x^(1/3)}, {x, -3, 3}, AspectRatio -> 1,
PlotLabels -> Automatic, Axes -> True,
AxesStyle -> Arrowheads[{0.0, 0.04}], AxesLabel -> {x, y},
ImageSize -> Medium, PlotHighlighting -> "XSlice"]
The correct image is
In[45]:= FunctionDomain[x^(1/3), x]
Out[45]= x >= 0
The Domain of a function of this function is also wrong