I want to generate a picture like this, highlight its outlines, don't show extra edges.
The built-in MengerMesh will have extra edges
mesh = MengerMesh[2, 3];
Graphics3D[{
{EdgeForm[], mesh},
{Thick, MeshPrimitives[mesh, 1]}
}, Boxed -> False]
I've tried the method here, It seems that it doesn't work for regions with holes.
Region`Mesh`MergeCells[BoundaryDiscretizeRegion@MengerMesh[2, 3]]
Inspired by chayong's answer, a direct way to identify the boundary edges using Region`Mesh`MeshCellNormals:
bmr = BoundaryMesh[MengerMesh[2, 3]];
boundaryedges = Pick[MeshPrimitives[bmr, 1],
Map[Unitize @ (1 - Max @ Abs @ #)&] @ RegionMeshMeshCellNormals[bmr, 1],1];
Show[bmr, Graphics3D[{AbsoluteThickness[3], boundaryedges}], Boxed -> False]
Alternatively, we identify the indices of boundary edges and highlight them using HighlightMesh:
boundaryindices = Pick[MeshCellIndex[bmr, 1][[All, 2]],
Map[Unitize @ (1 - Max @ Abs @ #)&] @ Region`Mesh`MeshCellNormals[bmr, 1], 1];
HighlightMesh[bmr,
Style[{1, boundaryindices}, Directive[Black, AbsoluteThickness[3]]]]
Combine co-planar faces and plot them using RegionPlot3D using the option BoundaryStyle:
bdm = BoundaryMesh @ MengerMesh[2, 3];
faces = MapApply[RegionUnion] @
Gather[MeshPrimitives[bdm, 2],
CoplanarPoints[Join[First @ #, First @ #2]] &];
RegionPlot3D[Evaluate @ faces,
Mesh -> None,
MaxRecursion -> 5,
BoundaryStyle -> Directive[Thick, Black],
Boxed -> False,
Lighting -> "Neutral",
ViewProjection -> "Orthographic",
ColorFunctionScaling -> False,
ColorFunction ->
(ColorData["BlueGreenYellow"][5/3
SquaredEuclideanDistance[{#, #2, #3}, {1, 1, 1}/2]] &)]
Remove the options ViewProjection,ColorFunctionScaling and ColorFunction to get
Get RegionMember function for MengerMesh[2,3] and use it with RegionPlot3D:
rmf = RegionMember @ MengerMesh[2, 3];
RegionPlot3D[rmf @ {x, y, z},
{x, 0, 1}, {y, 0, 1}, {z, 0, 1},
Mesh -> None,
MaxRecursion -> 5,
PlotPoints -> 200,
Boxed -> False, Axes -> False,
BoundaryStyle -> Thick, Lighting -> "Neutral"]
Note that, unlike the first method above, this method fails to style the interior edges.
Updated
BoundaryMesh is not needed, faster than the previous version
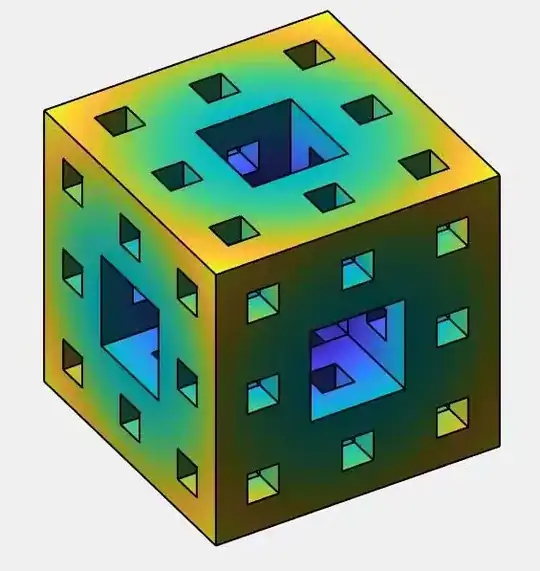
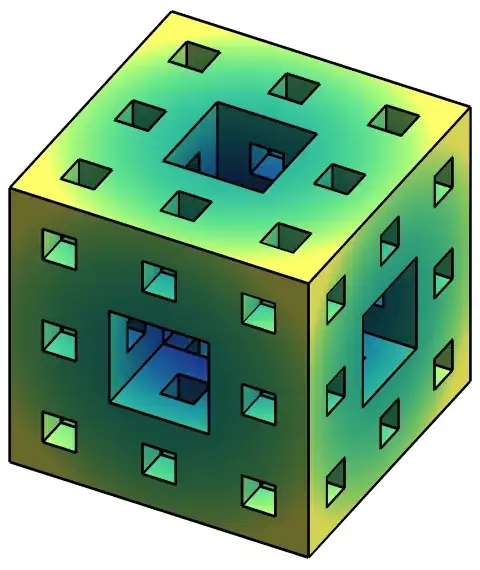
mesh = MengerMesh[4, 3];
idx = {1, 2, 2, 3, 3, 4, 4, 1, 5, 6, 6, 7, 7, 8, 8, 5, 1, 5, 2, 6, 3, 7, 4, 8};
outlines = MeshPrimitives[mesh, 3][[All, 1, idx]] //
RightComposition[
ArrayReshape[#, {Times @@ Dimensions@#/6, 2, 3}] &,
Map[Sort],
Tally,
Cases[{x_, 1} :> x],
Developer`ToPackedArray,
Line
]; // AbsoluteTiming
Graphics3D[{
{EdgeForm[], mesh},
{Black, Tube[outlines, Scaled[1/1000]]}
}, Boxed -> False, ImageSize -> 800, Lighting -> "Classic"]
{3.31279, Null}
Using method in Extract 2D quad mesh from 3D hexahedral mesh, add some optimization
Clear[boundaryMeshOutlines];
boundaryMeshOutlines[bmr_BoundaryMeshRegion, tol_ : 0.] :=
Module[{enormal, graph, edges, vl, adj, corneredges},
enormal = Region`Mesh`MeshCellNormals[bmr, 2];
graph = MeshConnectivityGraph[bmr, {1, 2}];
edges = MeshCellIndex[bmr, 1];
vl = VertexList[graph];
adj = Lookup[AssociationThread[vl, Extract[vl,
List/@ AdjacencyMatrix[graph]["AdjacencyLists"]]], edges][[All, All, 2]];
corneredges = Pick[edges, UnitStep[(Dot @@ enormal[[#]] & /@ adj) - 1 + tol], 0];
MeshPrimitives[bmr, corneredges, "Multicells" -> True]
];
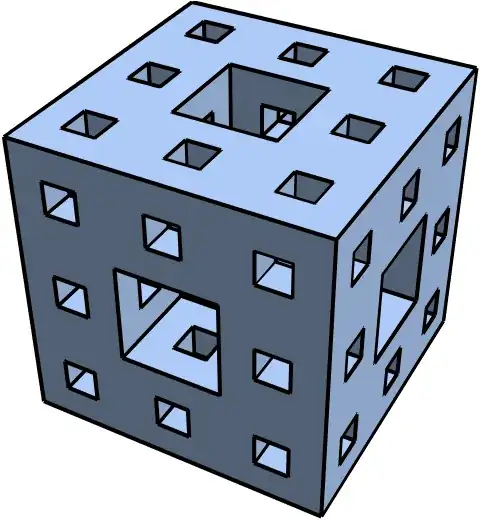
bmesh = BoundaryMesh[MengerMesh[3, 3]];
outlines = boundaryMeshOutlines[bmesh]; // AbsoluteTiming
Graphics3D[{
{EdgeForm[], bmesh},
{Black, Tube[#, Scaled[1/800]] & /@ outlines}
}, Boxed -> False, ImageSize -> 600]
{0.30785, Null}
It also works for this Construct a polyhedron from the coordinates of its vertices and calculate the area of each face
q={{-10.,-7.5,-6.25},{-10.,-7.5,6.25},{-10.,0.,-10.},{-10.,0.,10.},{-10.,7.5,-6.25},{-10.,7.5,6.25},{-1.66667,-11.6667,-8.33333},{-1.66667,-11.6667,8.33333},{2.5,-13.75,0.},{-2.5,0.,-13.75},{1.66667,-8.33333,-11.6667},{-2.5,0.,13.75},{1.66667,-8.33333,11.6667},{-1.66667,11.6667,-8.33333},{1.66667,8.33333,-11.6667},{-1.66667,11.6667,8.33333},{1.66667,8.33333,11.6667},{2.5,13.75,0.},{10.,-10.,0.},{10.,-6.25,-7.5},{10.,-6.25,7.5},{10.,6.25,-7.5},{10.,6.25,7.5},{10.,10.,0.}};
bdm=BoundaryMesh@DelaunayMesh[q];
Graphics3D[{
{EdgeForm[], bdm},
{Black,
Tube[#, Scaled[1/800]] & /@ boundaryMeshOutlines[bdm, 10^-5.]}
}, Boxed -> False, ImageSize -> 600]
