Plotting regions with zero eigenvalues of a matrix

Question

I have a series of matrices exemplify as

\begin{align} Atmp=\left( \begin{array}{cccccccc} 0. & 0. & 1.\, +0.5 e^{-i z} & 0. & 1. y+0.2 & 0.\, +0.75 i & 0. & 0. \\ 0. & 0. & 0. & -1.-0.5 e^{-i z} & 0.\, +0.75 i & 1. y-0.2 & 0. & 0. \\ 1.\, +0.5 e^{i z} & 0. & 0. & 0. & 0. & 0. & 0.2\, -1. y & 0.\, -0.75 i \\ 0. & -1.-0.5 e^{i z} & 0. & 0. & 0. & 0. & 0.\, -0.75 i & -1. y-0.2 \\ 1. y+0.2 & 0.\, -0.75 i & 0. & 0. & 0. & 0. & 1.\, +0.5 e^{-i z} & 0. \\ 0.\, -0.75 i & 1. y-0.2 & 0. & 0. & 0. & 0. & 0. & -1.-0.5 e^{-i z} \\ 0. & 0. & 0.2\, -1. y & 0.\, +0.75 i & 1.\, +0.5 e^{i z} & 0. & 0. & 0. \\ 0. & 0. & 0.\, +0.75 i & -1. y-0.2 & 0. & -1.-0.5 e^{i z} & 0. & 0. \\ \end{array} \right) \end{align}

which can be added to the Mathematica using

Atmp = {{0., 0., 1. + 0.5 E^(-I z), 0., 0.2 + 1. y, 0. + 0.75 I, 0., 
    0.}, {0., 0., 0., -1. - 0.5 E^(-I z), 0. + 0.75 I, -0.2 + 1. y, 
    0., 0.}, {1. + 0.5 E^(I z), 0., 0., 0., 0., 0., 0.2 - 1. y, 
    0. - 0.75 I}, {0., -1. - 0.5 E^(I z), 0., 0., 0., 0., 
    0. - 0.75 I, -0.2 - 1. y}, {0.2 + 1. y, 0. - 0.75 I, 0., 0., 0., 
    0., 1. + 0.5 E^(-I z), 0.}, {0. - 0.75 I, -0.2 + 1. y, 0., 0., 0.,
     0., 0., -1. - 0.5 E^(-I z)}, {0., 0., 0.2 - 1. y, 0. + 0.75 I, 
    1. + 0.5 E^(I z), 0., 0., 0.}, {0., 0., 0. + 0.75 I, -0.2 - 1. y, 
    0., -1. - 0.5 E^(I z), 0., 0.}};

Here is the plot of all eigenvalues.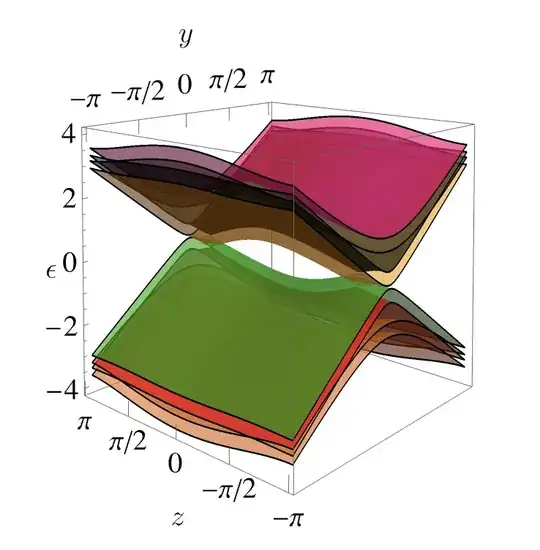. The figure can be generated using

L=30;
r1 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[1]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r2 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[2]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r3 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[3]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r4 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[4]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r5 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[5]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r6 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[6]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r7 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[7]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
r8 = Table[{y, z, 
    Re[Sort[Chop[Eigenvalues[Atmp]]][[8]]]}, {y, -\[Pi], \[Pi], 
    Pi/L}, {z, -Pi + 0.01, Pi, Pi/L}];
g1 = ListPlot3D[Flatten[r1, 1], 
   PlotStyle -> Directive[blue, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g2 = ListPlot3D[Flatten[r2, 1], 
   PlotStyle -> Directive[orange, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g3 = ListPlot3D[Flatten[r3, 1], 
   PlotStyle -> Directive[Red, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g4 = ListPlot3D[Flatten[r4, 1], 
   PlotStyle -> Directive[Green, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g5 = ListPlot3D[Flatten[r5, 1], 
   PlotStyle -> Directive[Yellow, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g6 = ListPlot3D[Flatten[r6, 1], 
   PlotStyle -> Directive[Black, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g7 = ListPlot3D[Flatten[r7, 1], 
   PlotStyle -> Directive[Gray, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
g8 = ListPlot3D[Flatten[r8, 1], 
   PlotStyle -> Directive[Magenta, Opacity[0.65]], Mesh -> False, 
   PlotRange -> All];
ticks = {{-[Pi], "-[Pi]"}, {-[Pi]/2, "-[Pi]/2"}, {0, 
    "0"}, {[Pi]/2, "[Pi]/2"}, {[Pi], "[Pi]"}};
Plothermitain = 
 Show[g1, g2, g3, g4, g5, g6, g7, g8, PlotRange -> All, 
  AspectRatio -> 1, BaseStyle -> {FontFamily -> "Times", 20}, 
  Frame -> True, Ticks -> {ticks, ticks, Automatic}, 
  AxesLabel -> {"y", "z", "E"}, ImageSize -> 250, 
  ImagePadding -> All]

In the $y-z$ plane, eigenvalues of my matrices exhibit some regions where two of the eigenvalues become zero and degenerate. My question is how to obtain the region numerically and plot it in the 2D y-z plane. Previously, some suggestions for obtaining these results when the symbolic equations of eigenvalues are given. However, here I don't have access to any symbolic expression.

The determinant of a matrix is the product of the eigenvalues. So the det is zero exactly when one (or more) of the eigenvalues are zero. Using this idea, you can do: det = Numerator[Det[Rationalize[Atmp]] // FullSimplify]; this gives a fairly simple expression in terms of y and z. This constructs a symbolic expression for when the eigenvalues are zero. — bill s, Jul 27 '23 at 14:16
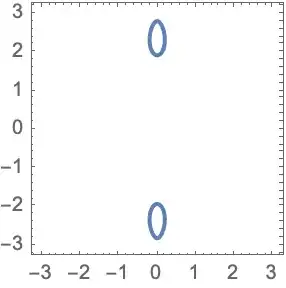
@bills Thanks for your nice suggestion. I have tried det = Numerator[Det[Rationalize[Atmp]] // FullSimplify] reSol = Reduce[{Re@det == 0, y \[Element] Reals, z \[Element] Reals}, {y, z}] RegionPlot@ ImplicitRegion[reSol, {{y, -\[Pi], \[Pi]}, {z, -\[Pi], \[Pi]}}] but it didn't work. — Shasa, Jul 27 '23 at 14:42

score 4 · Accepted Answer · answered Jul 27 '23 at 15:09

We can rationalize the matrix and calculate its symbolic eigenvalues:

ev = Eigenvalues@Rationalize@Atmp;

We can then explore these eigenvalues to qualitatively seek the ones that go to zero and are degenerate as follows. Note that working with arbitrary precision seems necessary here to obtain accurate and complete contours:

ContourPlot[# == 0, {y, -Pi, Pi}, {z, -Pi, Pi}, WorkingPrecision -> 10] & /@ ev

So eigenvalues (1 and 4), and (5 and 8) seem to be the ones of interest, in two degenerate pairs. Let's focus on those:

ContourPlot[
  ev[[{1, 5}]] == 0, {y, -Pi, Pi}, {z, -Pi, Pi},
  FrameLabel -> (Style[#, 14, Black] & /@ {"y", "z"}),
  FrameTicks -> {{Range[-Pi, Pi, Pi/2], None}, {Range[-Pi, Pi, Pi/2], None}},
  WorkingPrecision -> $MachinePrecision, PlotPoints -> 20
]

This is an excellent response! Thank you very much (+1). – Shasa Jul 27 '23 at 15:29 — Shasa, Jul 27 '23 at 15:29

score 3 · Answer 2 · answered Jul 27 '23 at 18:23

3

Following up on my comment, the determinant of a matrix is the product of the eigenvalues. So the det is zero exactly when one (or more) of the eigenvalues are zero. Using the ContourPlot from MarcoB's answer, then yields

p = Numerator[Det[Rationalize[Atmp]]//FullSimplify]; 
(ContourPlot[# == 0, {y, -Pi, Pi}, {z, -Pi, Pi}] & /@ p)[[1]]

answered Jul 27 '23 at 18:23

bill s

68,936
4
101
191

This is very nice! Thank you for sharing that(+1). – Shasa Jul 28 '23 at 06:56

Plotting regions with zero eigenvalues of a matrix

2 Answers2