Suppose I have a list like
{
{x1,y1,z1},
{x2,y2,z2},
{x3,y3,z3},
...
}
and I want to change it to
{
{x1+Cos[z1/x1],y1,z1-Sin[z1/x1]},
{x2+Cos[z2/x2],y2,z2-Sin[z2/x2]},
{x3+Cos[z3/x3],y3,z3-Sin[z3/x3]},
...
}
What is the best way to do these matrix manipulations?
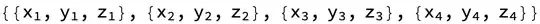

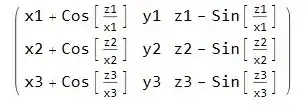
{#[[1]]+Cos[#[[2]]/#[[1]], #[[2]], #[[3]] - Sin[#[[3]]/#[[1]]]]}& /@ list– Daniel Huber Jul 27 '23 at 17:25