Plotting histogram from a list of bin boundaries and counts V2

Question

I would like to ask the very same question as Plotting histogram from a list of bin boundaries and counts, because I do not find it sufficiently answered.

"If I use HistogramList (in mathematica) to create list of bin boundaries and bin counts from my data, can I use this list to plot histogram? I want to add the counts from various datasets before plotting my final histogram. So, I would like an answer to my question." Is it possible to precalculate the bin counts and directly use them in the Histogram function?

In the answer to the cited and closed question a reference is made to the help file, where it is proposed that using the BarChart[Last[HistogramList[data]]] yields the same result as Histogram[data], which clearly isn't the case because the horizontal axis labeling is missing.

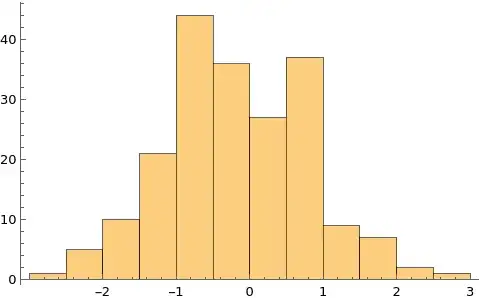
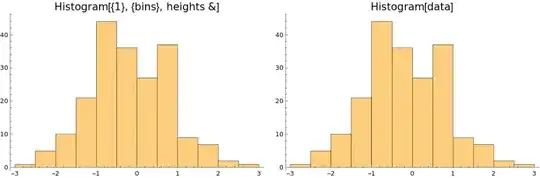
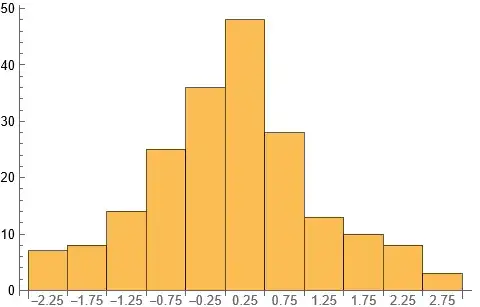
Thank you for this link, it certainly does. It can also be achieved by my following proposition: myhistogram2[hl_, options_] := ListLinePlot[{{#[[1]], 0}, {#[[1]], #[[2]]}} & /@ Transpose@{MovingAverage[hl[[1]], 2], Table[ Total[hl[[2, ;; , i]]] , {i, 1, Length@(hl[[2, 1, ;;]])}] }, PlotStyle -> Orange, options]
But it seems there is no native solution to it. Thanks for the quick reply! — ango4, Jul 28 '23 at 15:31

kglr · Answer 1 · 2023-07-29T01:40:06.143

4

You can use bin lists and counts returned by HistogramList as the second and third arguments in Histogram (with arbitrary fake data in the first argument):

SeedRandom[12345];
data = RandomVariate[NormalDistribution[], 200];
{bins, heights}  = HistogramList[data];
Histogram[{1}, {bins}, heights &]

Row[{
   Histogram[{1}, {bins}, heights &, 
      PlotLabel -> Style["Histogram[{1}, {bins}, heights &]", Black, 16],
      ImageSize -> 400], 
  Histogram[data, PlotLabel -> Style["Histogram[data]", Black, 16],
      ImageSize -> 400]}, 
  Spacer[10]]

Same method works for Histogram3D:

SeedRandom[12345];
data2d = RandomVariate[NormalDistribution[], {200, 2}];
{bins2d, heights2d} = HistogramList[data2d];
Row[{Histogram3D[{{1, 2}}, List /@ bins2d, heights2d &, 
   PlotLabel -> 
    Style["Histogram3D[{{1,2}}, List/@bins2d, heights2d&]", Black, 16], 
  ImageSize -> 400], 
 Histogram3D[data2d, ImageSize -> 400, 
   PlotLabel -> Style["Histogram3D[data2d]", Black, 16]] }, 
 Spacer[10]]

edited Jul 29 '23 at 01:40

answered Jul 29 '23 at 01:07

kglr

394,356
18
477
896

2

Wow! That is short and sweet. I see that {1} can be replaced with any list of numbers (real and even complex numbers!). So Histogram essentially ignores the first argument when heights is followed by & ? – JimB Jul 29 '23 at 01:20
1

@JimB, yes, and same trick works for Histogram3D. – kglr Jul 29 '23 at 01:34
1

Thank you @kglr! This is exactly what answers the question. It should be suggested to be added to the official documentation, because it fills exactly the missing link. – ango4 Jul 29 '23 at 10:06

score 3 · Accepted Answer · answered Jul 28 '23 at 16:46

One can use WeightedData with Histogram to obtain a histogram.

(* Generate some data and a histogram list *)
SeedRandom[12345];
data = RandomVariate[NormalDistribution[], 200];
hlist = HistogramList[data];
(* Centers of bins *)
x = Table[(hlist[[1, i]] + hlist[[1, i - 1]])/2, {i, 2, Length[hlist[[1]]]}];
(* Plot the histogram *)
Histogram[WeightedData[x, hlist[[2]]], {hlist[[1]]}]

As a check construct a histogram with the raw data and same bin boundaries:

Histogram[data, {hlist[[1]]}]

score 2 · Answer 3 · answered Jul 28 '23 at 16:30

The reason for wanting to use BarChart isn't stated but if there's some need to do so, you can get essentially the same result as Histogram.

data = RandomVariate[NormalDistribution[], 200];
hlist = HistogramList[data];
labels = Table[ToString[(hlist[[1, i]] + hlist[[1, i - 1]])/2 // N], {i, 2,  Length[hlist[[1]]]}];
BarChart[Last[hlist], BarSpacing -> None, ChartLabels -> labels]

Plotting histogram from a list of bin boundaries and counts V2

3 Answers3

Linked