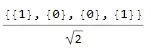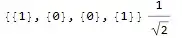3

This is a follow-up question to answer given by iPoiler on the original question, "Factoring out a common term". The function FactorByVariable works great for polynomials, but not for a matrix. For example, I would like to factor out 1/Sqrt[2] from the matrix {{1/Sqrt[2]},{0},{0},{1/Sqrt[2]}}. The function FactorByVariable went through the necessary steps. Howver, the last step simplify the intermediate step, (1/Sqrt[2])Expand[{{1},{0},{0},{1}}] to the original expression. I started to study Quantum Computing. Factoring out a common term from a matrix (or tensor) is quite important. Any help will be very much appreciated.

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198
Sang Dhong
  • 61
  • 3
  • 1
    Do you have a link to the "original question"? Please edit the question and add it. – Michael E2 Aug 08 '23 at 02:02
  • 3
    Does this help? https://mathematica.stackexchange.com/questions/70131/extract-common-factor-from-vector-or-matrix – ydd Aug 08 '23 at 02:07
  • 3
    Also related: https://mathematica.stackexchange.com/questions/267910/factor-out-common-terms-from-a-list-of-terms – Michael E2 Aug 08 '23 at 02:08

1 Answers1

2

You may extract the common factor in several ways. E.g. Using "Extract" if you know the position otr simply by replacing the common factor by 1.

However, the problem here is, if you have extracted the common factor, MMA will at once multiply it back and you are where you started. Therefore, you must wrap the simplified matrix into "HoldForm". However, this will prevent the extraction and you must force the extraction inside "HoldForm" by "Evaluate":

m = {{1/Sqrt[2]}, {0}, {0}, {1/Sqrt[2]}};
1/Sqrt[2] HoldForm[Evaluate[m /. 1/Sqrt[2] -> 1]]

enter image description here

This is not yet complete satisfactorily. You may also wrap 1/Sqrt2 with HoldForm:

HoldForm[1/Sqrt[2]] HoldForm[Evaluate[m /. 1/Sqrt[2] -> 1]]

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57