Documented or undocumented?
According to the docs(!), GroebnerBasis[Thread[Equal[{x,y,z},expr]],{},t] treats the expressions as polynomials in t with the omitted variables x, y, z treated as "parameter variables." According to the docs, the parameter variables will be inferred from variables missing in the specified variables, if they are not explicitly declared with the ParameterVariables option. The following give the same output:
GroebnerBasis[{x, y, z} - expr, {x, y, z}, t,
MonomialOrder -> EliminationOrder]
(* {-1 + x^2 + y^2 + z^2, -3 Sqrt[3] x y + z^3} *)
GroebnerBasis[{x, y, z} - expr, {t, x, y, z}, t,
MonomialOrder -> EliminationOrder, ParameterVariables -> {x, y, z}]
(* {-1 + x^2 + y^2 + z^2, -3 Sqrt[3] x y + z^3} *)
The above basis is not the same as but is clearly equivalent to the basis returned in one of the OP's codes:
GroebnerBasis[{x, y, z} - expr, {}, t]
(* {9 x y - Sqrt[3] z^3, -1 + x^2 + y^2 + z^2} *)
As others have mentioned, the basis depends on the ordering. See for instance Monomial Order or google it. Specifying {x, y, z} puts x first, so, for example, the first element of the basis has the lowest degree in x (zero, in this case). If you specify the order {y, z, x}, then the first element of the basis has the lowest degree in y. This is not the only property of a Groebner basis, of course, and it is meant to point out only that the order of the variables makes a difference.
Also, there are (at least) three types of variables, ordinary ones, ones to be eliminated, and parameter variables. And despite the documentation implying that omitted variables are treated like explicitly declared ParameterVariables, it is unclear to me that that is actually true. A possible fourth type of variable are the numeric constants that are not strictly speaking numbers. In the OP's problem, that includes Sqrt[3]. How these types affect the algorithm is unknown to me.
Where the difference turns up
There is an undocumented internal function that can reduce the basis. For instance, GroebnerBasis[{x, y, z} - expr, {}, t] first produces the GroebnerBasis[{x, y, z} - expr, {x, y, z}, t] basis, and then calls the following:
GroebnerBasis`Interreduce[
{-27 y^2 + 27 y^4 + 27 y^2 z^2 + z^6, -3 Sqrt[3] y + 3 Sqrt[3] y^3 +
3 Sqrt[3] y z^2 + x z^3, 9 x y - Sqrt[3] z^3, -1 + x^2 + y^2 + z^2},
{}, t,
{CoefficientDomain -> RationalFunctions, Modulus -> 0,
MonomialOrder -> Lexicographic, ParameterVariables -> {},
Tolerance -> 0}]
(* {9 x y - Sqrt[3] z^3, -1 + x^2 + y^2 + z^2} *)
Some types of variables:
traceDump1 = Trace[
GroebnerBasis[{x, y, z} - expr, {}, t],
TraceInternal -> True];
DeleteDuplicates@
Cases[traceDump1,
_Solve`SolvVar | _Solve`ElimVar | _Solve`ParmVar |
_Solve`RecipVar | _Solve`RadVar,
Infinity]
(*
{Solve`ElimVar[t], Solve`RecipVar[1/(1 + Solve`ElimVar[t]^2)],
Solve`SolvVar[x], Solve`SolvVar[y], Solve`ParmVar[Sqrt[3]],
Solve`SolvVar[z]}
*)
You can see how the variables are tagged. Some of these are eliminated as the given system is converted to a polynomial system (such as RecipVar[]). Note that x, y, and z are not tagged ParmVar[]; but they are if you specify ParameterVariables -> {x, y, z}. It's not clear whether these tags are used in computing the basis or only in preprocessing the input.
The square-root variable
It may be surprising that Sqrt[3] is treated as a variable. For that reason, I wish to point out a couple of things that might not be of central importance to the OP's question.
You can include Sqrt[3] in the list of variables. For instance, {x, Sqrt[3], y, z} gives a different Groebner basis than {x, y, z}. If we include it in the variables to be eliminated, the result is disappointing and has the wrong dimension (maybe a bug?):
GroebnerBasis[{x, y, z} - expr, {x, y, z}, {t, Sqrt[3]}]
(* {-1 + 3 x^2 - 3 x^4 + x^6 + 3 y^2 + 21 x^2 y^2 + 3 x^4 y^2 - 3 y^4 +
3 x^2 y^4 + y^6} *)
But I've had trouble with over-eliminating before. If we're going to eliminate two variables, I should start with four equations. But it's hard to get a rational polynomial relation for Sqrt[3] that does not automatically evaluate to 0; for instance Sqrt[3]^2 - 3 does not work. But we can use an indirect method:
GroebnerBasis[
Join[{x, y, z} - expr, {a - Sqrt[3], a^2 - 3}],
{x, y, z}, {t, Sqrt[3], a}]
(* {-27 y^2 + 27 y^4 + 27 y^2 z^2 + z^6, -1 + x^2 + y^2 + z^2} *)
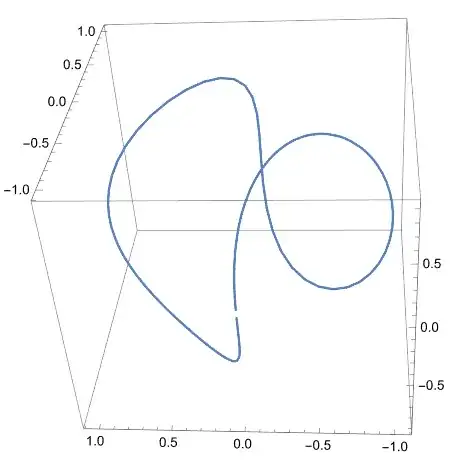
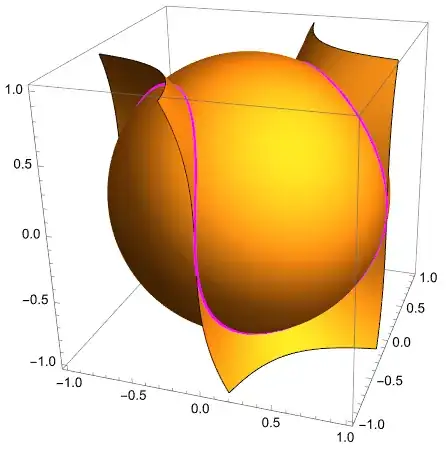





GroebnerBasis, does it? – yode Aug 19 '23 at 07:30Eliminate[Thread[Equal[{x,y,z},expr]],t]– yode Aug 19 '23 at 08:40