NIntegrate extremely piecewised functions

Question

I often need to integrate extremely piecewised functions, like the following one (not extreme, but gives an idea):

q[time_?NumericQ] := 
 Module[{q1 = 0.7, d1 = 600, p1 = 2700, ph1 = 0, q2 = 0.37, d2 = 870.,
    p2 = 5000, ph2 = 0},
  If[Mod[time, p1] > ph1 && Mod[time, p1] < ph1 + d1, q1, 0] + 
   If[Mod[time, p2] > ph2 && Mod[time, p2] < ph2 + d2, q2, 0]]

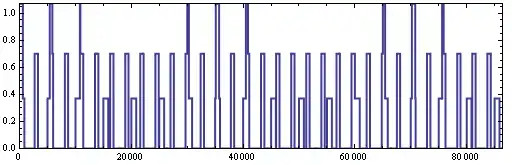
I know that I can list all the mandatory points in the NIntegrate interval List. But most of the time I don't know them.

Running NIntegrategenerally returns singularity, accuracy, etc, type of errors.

NIntegrate[q[t], {t, 0, 7*24*3600}]

I can play around with WorkingPrecision, MaximumRecursion, etc, but it is not that easy to arrive at something that returns no errors, or that runs in a reasonable time.

I generally end up running something like:

NIntegrateBis[funct_, list_] := 
 Module[{step = 0.1, time = list[[1]], int = 0}, 
  While[time < list[[2]], int = int + funct[time]*step; 
   time = time + step]; int]

NIntegrateBis[q, {0, 10000}]

Simple and with no messages... but no error control, no variable step, etc (it can even overpass the boundaries, although it is easy to correct that part...)

What is the best strategy to integrate my functions? Use NIntegrate with a specific set of options (that I don't know of)? Build a personal NIntegrate?

PS - I'm running optimization simulations with those functions, and so, I need it to run pretty fast.

Answer 1

Assuming the discontinuities in your function cannot be studied symbolically (which is the case in your example due to the inclusion of _?NumericQ), you will indeed need to roll something by hand to solve this efficiently. The built-in strategies for NIntegrate are suitable for piecewise smooth functions where the piecewise behavior can be elicited from the symbolic structure of the integrand.

Essentially you need to create a FindAllDiscontinuities function that attempts to find all function discontinuities numerically. This is only possible if you can make some assumptions about the scale of the discontinuities, which perhaps you can in your real scenario.

A rough outline of the function would be to first evenly, densely* sample the function into small sub-regions, then recursively bisect these until you are convinced* they look smooth: As you bisect, if the apparent function slope increases instead of staying roughly constant, you probably have a discontinuity.

*The asterisks are parameters that depend on the expected behavior of your real function.

Answer 2

Neither fast nor slow, but it gives no errors. Originally I used PiecewiseExpand to convert the function before passing it to NIntegrate. But it turns out NIntegrate will do it for me, if I remove the ?NumericQ from the definition of q and raise the $MaxPiecewiseCases limit to let NIntegrate do some symbolic processing.

q[time_] := 
 Module[{q1 = 0.7, d1 = 600, p1 = 2700, ph1 = 0, q2 = 0.37, d2 = 870., p2 = 5000, ph2 = 0}, 
   If[Mod[time, p1] > ph1 && Mod[time, p1] < ph1 + d1, q1, 0] + 
    If[Mod[time, p2] > ph2 && Mod[time, p2] < ph2 + d2, q2, 0]];

Block[{$MaxPiecewiseCases = 500},
  NIntegrate[q[t], {t, 0, 7*24*3600}]
  ] // AbsoluteTiming
(*
   {4.384593, 133030.}
*)

Answer 3

Another possibility is to use NDSolveValue to integrate your function:

NDSolveValue[
    {i'[t]==q[t],i[0]==0},
    i[7 24 3600],
    {t,0,7 24 3600},
    MaxStepFraction->0.0005
] //AbsoluteTiming

{1.38051, 133030.}

in agreement with @MichaelE2's answer.

Answer 4

One can try to average the function say, on $[0,50000]$ with step 100 (and compile to get better performance): $$ f(t)=\sum_{k=0}^{5\cdot10^2-1} q(t+100k) $$

f = Compile[{{time, _Real}},
   Sum[
    Module[{q1 = 0.7, d1 = 600, p1 = 2700, ph1 = 0, q2 = 0.37, 
      d2 = 870., p2 = 5000, ph2 = 0}, 
     If[Mod[tt, p1] > ph1 && Mod[tt, p1] < ph1 + d1, q1, 0] + 
      If[Mod[tt, p2] > ph2 && Mod[tt, p2] < ph2 + d2, q2, 0]], {tt, 
     time, time + 5 10^4 - 100, 100}]
   ];

hoping the result will be "less piecewise".

Plot[f[x], {x, 0, 100}]

Trying to integrate f gets the result, still producing error messages though. But since the integrand is not smooth, the precision to be had directly depends on number of points at which the function is evaluated. One can play here with methods/parameters/precision, of course, to obtain better results.

Answer 5

In my case, just using Compile speeds up everything pretty much. The speed up gain is more than 100 times.

q2 = Compile[{{time, _Real}}, With[{q1 = 0.7, d1 = 600, p1 = 2700, ph1 = 0, q2 = 0.37, d2 = 870., p2 = 5000, ph2 = 0}, If[Mod[time, p1] > ph1 && Mod[time, p1] < ph1 + d1, q1, 0] + If[Mod[time, p2] > ph2 && Mod[time, p2] < ph2 + d2, q2, 0]], CompilationTarget -> "C"];

NIntegrateBis2 = Compile[{{list1, _Real}, {list2, _Real}}, Block[{step = 0.1, time = list1, int = 0.0}, While[time < list2, int = int + q2[time]*step; time = time + step]; int], CompilationTarget -> "C"];

In[14]:= NIntegrateBis2[0, 10000] // Timing
Out[14]= {0.028000, 2323.69}