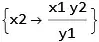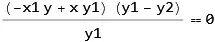How to replace polynomials numerically?

Question

We know that the value of this equation is 0

x2 y1 - x1 y2 == 0

For the following equation, there is a correlation between the polynomial parts of the known equation (opposite to each other).

-x1 y + x2 y + x y1 - x2 y1 - x y2 + x1 y2 == 0

Why can't the replacement be replaced with 0?

(-x1 + x2) y - x2 y1 + x (y1 - y2) + x1 y2 == 0 /. (x2 y1 - x1 y2) -> 
  0

Since you can read Chinese, check this also: https://note.youdao.com/noteshare?id=77b86cb08aaf29ce8747990c9e717298 — xzczd, Aug 18 '23 at 06:54

score 4 · Accepted Answer · answered Aug 18 '23 at 06:38

4

Simplify[x1 y + x2 y + x y1 - x2 y1 - x y2 + x1 y2, 
 x2 y1 - x1 y2 == 0]

x1 y + x2 y + x (y1 - y2).

answered Aug 18 '23 at 06:38

cvgmt

72,231
4
75
133

score 2 · Answer 2 · answered Aug 18 '23 at 06:37

2

You can solve it and replace it in the second, likeso:

sltn1 = Solve[x2 y1 - x1 y2 == 0][[1]];
DivideSides[
  Factor[(-x1 y + x2 y + x y1 - x2 y1 - x y2 + x1 y2 == 0) /. sltn1], 
  x1, Assumptions -> {x1 != 0}] // FullSimplify

answered Aug 18 '23 at 06:37

bmf

15,157
2
26
63

score 1 · Answer 3 · answered Aug 18 '23 at 06:46

Side relation can be used (sometimes) but often they fail.

An alternative is to solve for one of the variables from the relation you want to use, and then replace that variable into the polynomial. This will always work. Like this

ClearAll["Global`*"]
p    = (-x1+x2) y-x2 y1+x (y1-y2)+x1 y2==0
side = (x2 y1-x1 y2)==0
x2Sol= First@Solve[side,x2]

Mathematica graphics

And now

p/.x2Sol//Simplify

Mathematica graphics

In this method, which variable to solve for is arbitrary.

How to replace polynomials numerically?

3 Answers3