How do I animate arms on my triple pendulum?

Question

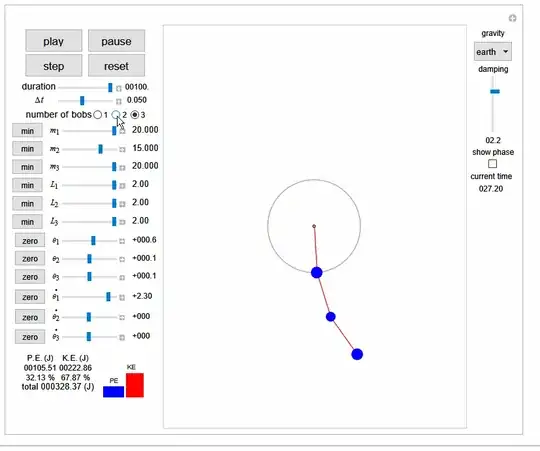
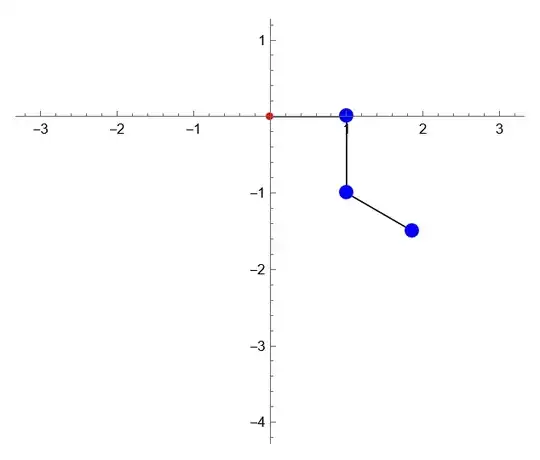
I have three Euler-Lagrange equations which describe the dynamics of a triple pendulum and I have managed to plot the pendulum's pivot points parametically but I cannot figure out how to put arms on the pendulum and make the plot look more realistic.

EDIT: Here is the full code.

Subscript[x, 1] = Subscript[l, 1] Sin[ Subscript[\[Theta], 1][t]];
Subscript[y, 1] = -Subscript[l, 1] Cos[Subscript[\[Theta], 1][t]];
Subscript[x, 2] = 
  Subscript[l, 1] Sin[ Subscript[[Theta], 1][t]] + 
   Subscript[l, 2] Sin[ Subscript[[Theta], 2][t]];
Subscript[y, 
  2] = -Subscript[l, 1] Cos[Subscript[[Theta], 1][t]] - 
   Subscript[l, 2] Cos[Subscript[[Theta], 2][t]];
Subscript[x, 3] = 
  Subscript[l, 1] Sin[Subscript[[Theta], 1][t]] + 
   Subscript[l, 2] Sin[Subscript[[Theta], 2][t]] + 
   Subscript[l, 3] Sin[Subscript[[Theta], 3][t]];
Subscript[y, 
  3] = -Subscript[l, 1] Cos[Subscript[[Theta], 1][t]] - 
   Subscript[l, 2] Cos[Subscript[[Theta], 2][t]] - 
   Subscript[l, 3] Cos[Subscript[[Theta], 3][t]];
K = 0.5 Subscript[m, 
    1] (D[Subscript[x, 1], t]^2 + D[Subscript[y, 1], t]^2) + 
   0.5 Subscript[m, 
    2] (D[Subscript[x, 2], t]^2 + D[Subscript[y, 2], t]^2) + 
   0.5 Subscript[m, 
    3] (D[Subscript[x, 3], t]^2 + D[Subscript[y, 3], t]^2);
V = g (Subscript[m, 1] Subscript[y, 1] + 
     Subscript[m, 2] Subscript[y, 2] + 
     Subscript[m, 3] Subscript[y, 3]);
L = K - V;
Partial1 = D[L, Subscript[[Theta], 1][t]];
Partial2 = D[L, Subscript[[Theta], 2][t]];
Partial3 = D[L, Subscript[[Theta], 1]'[t]];
Partial4 = D[L, Subscript[[Theta], 2]'[t]];
Partial5 = D[L, Subscript[[Theta], 3][t]];
Partial6 = D[L, Subscript[[Theta], 3]'[t]];
EulerLagrange1 = 0 == FullSimplify[Partial1 - D[Partial3, t]];
EulerLagrange2 = 0 == FullSimplify[Partial2 - D[Partial4, t]];
EulerLagrange3 = 0 == FullSimplify[Partial5 - D[Partial6, t]];
Subscript[m, 1] = 1;
Subscript[m, 2] = 1;
Subscript[m, 3] = 1;
g = 1;
Subscript[l, 1] = 1;
Subscript[l, 2] = 1;
Subscript[l, 3] = 1;
timelimit = 6;
Subscript[initial[Theta], 1] = Pi/2;
Subscript[initial[Theta], 2] = 0;
Subscript[initial[Theta], 3] = Pi/3;
solution = 
  NDSolve[{EulerLagrange1, EulerLagrange2, EulerLagrange3, 
    Subscript[[Theta], 1][0] == Subscript[initial[Theta], 1], 
    Subscript[[Theta], 2][0] == Subscript[initial[Theta], 2], 
    Subscript[[Theta], 3][0] == Subscript[initial[Theta], 3], 
    Subscript[[Theta], 1]'[0] == 0, Subscript[[Theta], 2]'[0] == 0, 
    Subscript[[Theta], 3]'[0] == 0}, {Subscript[[Theta], 1], 
    Subscript[[Theta], 2], Subscript[[Theta], 3]}, {t, 0, 
    timelimit}];
Animate[ParametricPlot[{{Subscript[x, 1], Subscript[y, 
     1]}, {Subscript[x, 2], Subscript[y, 2]}, {Subscript[x, 3], 
     Subscript[y, 3]}} /. solution, {t, 0, tend}, 
  PlotRange -> {{-4, 4}, {-4, 4}}, AxesLabel -> {"x (m)", "y (m)"}, 
  PlotLabel -> "Pendulum trajectory"], {tend, 0, timelimit}, 
 AnimationRepetitions -> 1]

I am trying to make it look like this GIF which was posted as a comment: https://www.12000.org/animation/pendulum/movie.gif

Apologies for the messy post, this is my first time using Mathematica and the first time I have used this forum.

My post is mostly code now so I need to add details.

Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details. Details.

I can't run your code since it is not complete. Do you mean you want to make pendulum with 3 bobs? something like this or do you mean something else? — Nasser, Aug 23 '23 at 13:06
Welcome to the Mathematica Stack Exchange. Please provide a minimal example as Mathematica code that can be copied, pasted and executed in our notebook sessions. Thanks. — Syed, Aug 23 '23 at 13:12
I have added the full code, I would like it to look just like the GIF you posted but I am unsure how. — Christopher, Aug 23 '23 at 15:54
Well, the gif I posted was written using Mathematica. I could post that code if you want. Much easier for me than fixing your code and figuring what it is doing. I also have hard time reading code with Subscripts — Nasser, Aug 23 '23 at 15:58

Nasser · Answer 1 · 2023-08-24T03:25:36.730

The code is a little large as it does many things and have many controls.

I do not remember when I wrote it but its been many years. I am surprised it still runs as is with no changes on Latest Mathematica! I expected to see some problems.

I put a link to the notebook pendulum_august_23_2023.nb since the code is very large.

Here is a link to pendulum_august_23_2023.m plain text version of the same code. It will not be easy to read as I copied the code using COPY AS PLAIN TEXT and not as INPUT TEXT (in order to prevent \ from being added due to line breaks).

Here it is

You can also change the mass of the bobs and the length of the arms

I tried to paste the code here, but stackexchange will not let me, as over the limit by few thousand characters. I do not know what to do about this, as it is all one function (Manipulate) and I can't split it. If someone has any idea how to do it, will try.

Introduction

The equations of motion of the pendulum were derived using the Lagrangian energy method. For the n-bob pendulum, there are n-second order nonlinear differential equations and n degrees of freedom.

The equations are kept in their non-linear form since NDSolve was used for the solving them.

Mathematica was used to do the analytical derivation due to the high complexity of algebra for the $n=3$ case.

Initial position conditions can be changed by dragging the bob using the mouse. When the mouse is clicked on the display, it will pause and then the mouse can be used to drag the bob to a new location.

Logic inside the Demonstration will detect which bob to drag based on the proximity of the mouse current location to known bob positions. Below is description of each control variable shown on the Demonstration: The top buttons Labeled 'run', 'pause', 'step' and 'reset' and self explanatory and used to control the simulation.

The control labeled 'duration' is used to set the maximum simulation time. When this time is reached, the simulation will restart again from t=0 automatically. The control labeled $\Delta t$ is used to change the time step for the display. The smaller the time step, the more accurate the simulation will be, but it will take longer to complete.

The control labeled 'number of bobs' is used to change the pendulum type to either simple, double or triple. The controls below that are used to adjust the mass of the bobs, units are in kg.

All units in this simulation are in SI units.

The controls below that are used to change the length of each pendulum bar. The controls below that are used to set the initial conditions.

Units are in radians for the angles and in radians per second for the angular velocities.

Initial angle positions can also be set using the mouse as mentioned above, however, using the controls might provide more accurate settings if needed. For convenience, small buttons next to the control variables can be used to quickly set the value to zero.

The 'g' control is used to select the gravitational constant g. The control labeled 'show phase' is used to turn on and off the phase portrait plot.

The red point in the phase portrait plot indicates the initial conditions, and the black point is the position at the end of the duration.

The moving blue point is the position in phase space at the current time. The control labeled 'c' is used to change the damping coefficient. At the bottom is a display of the energy plot, it shows the current kinetic energy (KE), potential energy (PE) and the total energy in Joules.

The angles $\theta_1,\theta_2,\theta_3$ are all measured from the vertical line.

When the pendulum is hanging vertically at rest, then all angles will have zero values at this position.

The angles and velocities are taken to be positive in anticlockwise direction.

Reference:

Dare A. Wells, Schaum's Lagrangian Dynamics, McGraw-Hill, 1967

If this is not what you wanted, just let me know so I can delete this post.

Could you perhaps provide a text-only code dump in eg PasteBin as well? — MarcoB, Aug 24 '23 at 01:43

cvgmt · Accepted Answer · 2023-08-24T11:50:59.313

Use the original code but maybe need to modify something.

ani = Animate[Block[{t = tend, pts},
   pts = {{0, 0}, {Subscript[x, 1], 
       Subscript[y, 1]}, {Subscript[x, 2], 
       Subscript[y, 2]}, {Subscript[x, 3], Subscript[y, 3]}} /. 
     solution[[1]];
   Graphics[{Line /@ Partition[pts, 2, 1], Brown, 
     AbsolutePointSize[5], Point@pts[[1]], AbsolutePointSize[5], Blue,
      Point@pts[[2]], AbsolutePointSize[8], Blue, Point@pts[[3]], 
     AbsolutePointSize[10], Blue, Point@pts[[4]]}, 
    PlotRange -> {{-4, 4}, {1, -8}}]], {tend, $MachineEpsilon, 
   timelimit}]

Combine with the tracks.

Clear[ani];
ani = Animate[
  Block[{pts = {{Subscript[x, 1], Subscript[y, 1]}, {Subscript[x, 2], 
         Subscript[y, 2]}, {Subscript[x, 3], Subscript[y, 3]}} /. 
       solution[[1]] // Evaluate},
   Show[ParametricPlot[pts // Evaluate, {t, 0, tend}, 
     PlotStyle -> Dashed], 
    Graphics[{Line /@ 
       Partition[Prepend[pts /. t -> tend, {0, 0}], 2, 1], Red, 
      AbsolutePointSize[5], Point[{0, 0}], Blue, 
      AbsolutePointSize[10], Point[pts /. t -> tend]}], 
    PlotRange -> {{-3, 3}, {1, -4}}, 
    AxesOrigin -> {0, 0}]], {tend, $MachineEpsilon, timelimit}]

This is Brilliant! Exactly what I envisioned, and the code required no modifications to work, thank you so much!
I still have some questions though. How can I make the dashed line disappear over time so that the trail only lasts ~three seconds. If I set timelimit to be a large number the pendulum runs very fast initially so how do I set the speed of the animation based on the timelimit? When the pendulum has been running for a long time with the dashed line trails, the dashed lines begin to wiggle about a bit, how can I make them more stable? — Christopher, Sep 01 '23 at 04:11

How do I animate arms on my triple pendulum?

2 Answers2

Introduction