Question
I want to calculate the FractionalD of an InterpolatingFunction object, however, evaluating
FractionalD[Interpolation[Range[5]][x],{x,1/2}]
evaluates the argument but FractionalD remains unchanged, returning
FractionalD[ InterpolatingFunction[(* Something *)] ]
I would have expected an InterpolatingFunction object, the same output as Interpolation[Sqrt[Range[5]]*2/Sqrt[Pi]]
How to calculate the fractional derivative of an InterpolatingFunction so the output is another InterpolatingFunction?
Background
Fractional Derivatives
On the one hand, Wolfram Language (Mathematica) is fully capable of performing symbolic calculations of Fractional Derivatives defined as
For example,using FractionalD, FractionalD[f[x],{x,α}] gives the Riemann–Liouville fractional derivative of order α of the function $f(x)$,
FractionalD[x,{x,1/2}]
Interpolating Functions
On the other hand, one can take derivatives of InterpolatingFunction objects using D and Derivative.
For example,
D[Interpolation[Range[9]][x],x]
Visually,
Plot[
Evaluate[
{
Interpolation[Range[5]][x],
D[Interpolation[Range[5]][x],x]
}
]
,{x,0, 3}
]
Due diligence
Web
I have searched the site and the web for the relevant keywords, unsuccessfully.
Piecewise (edited)
Thanks to @MichaelE2way for pointing out that @CarlWoll 's InterpolationToPiecewise transforms an InterpolatingFunction (only "Hermite" Method) into a Piecewise object. In that particular case, the answer would be more straightforward, as FractionalD does evaluate over Piecewise functions and one could re-build the InterpolatingFunction with FunctionInterpolation. I'm still interested in alternative solutions.
NFractionalD
It seems NFractionalD does work with InterpolatingFunction
NFractionalD[Interpolation[Range[9]][x], {x, 1/2}, 0.25]
But that would imply that I need to deconstruct the InterpolatingFunction to extract the data points to use NFractionalD in each point to then build a new InterpolatingFunction using Interpolation. That looks too cumbersome and error-prone.

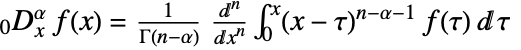



NFractionalDdoes work, this seems like an oversight from Wolfram Research,FractionalDshould work onInterpolatingFunctionnatively. – rhermans Aug 25 '23 at 10:37InterpolatingFunctiondefined by crossing points, but not by its derivatives, like this smooth staircaseInterpolation[Table[{{x},x,0,0,0,0},{x,0,9}]]. – rhermans Aug 25 '23 at 12:37InterpolationToPiecewiseseems to give the exact form for whatever is the underlying interpoation order. I think my answer does order 3 only. – Michael E2 Aug 25 '23 at 16:25