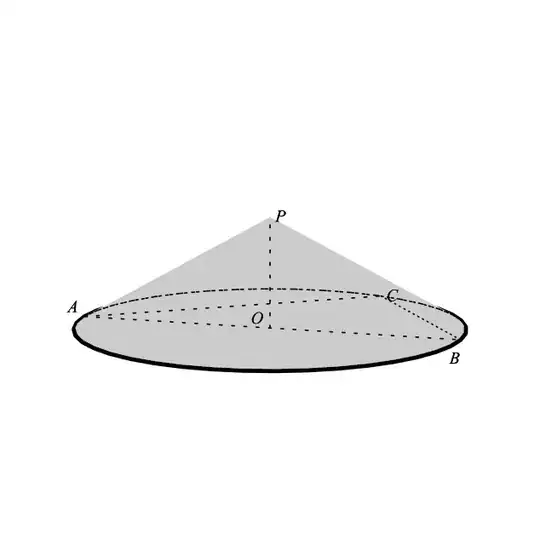
The vertex of the cone is P, the center of the base circle is O, AB is the diameter of the base, the angle APB is 120 degrees, AP=2, point C is on the circumference of the base, and the dihedral angle P-AC-O is 45 degrees
How can drawing this cone always show code running?
Clear["Global`*"];
r=Sqrt[3];h=1;
o={0,0,0};p={0,0,h};\[Alpha]=180 Degree;
circle[t_]=r {Cos[t],Sin[t],0};
b=circle[0];
a=circle[0+\[Alpha]];
c={x,y,z};
c=SolveValues[{(c-a) . (b-c)==0,Abs[Cos[VectorAngle[Cross[p-a,p-c],Cross[a-o,a-c]]]]==Cos[45 Degree],z==0},{x,y,z}]//First
labels={Text[Style[O,12,FontFamily->"Times"],o,{2,-1}],Text[Style[A,12,FontFamily->"Times"],a,{2,-1}],Text[Style[B,12,FontFamily->"Times"],b,{1,2}],Text[Style[C,12,FontFamily->"Times"],c,{-2,0}],Text[Style[P,12,FontFamily->"Times"],p,{-2,0}]};
cir=ParametricPlot3D[circle[t],{t,0,2 \[Pi]},Mesh->{{\[Pi]}},MeshShading->{Directive@{Dashed,Black},Black}];
dashLines={Dashed,AbsoluteThickness[2],Line[{{o,p},{a,b},{a,c},{b,c}}]};
realLines={AbsoluteThickness[2],Line[{{a,p},{b,p}}]};
boundaryLines={AbsoluteThickness[2],Line[{{a,p},{b,p}}]};
Show[Graphics3D[{dashLines,realLines,boundaryLines,labels}],cir,Boxed->False,Axes->False,ViewPoint->{-0.29,-3.26,0.84}]