How can I find all integer numbers so that mydistance is an integer number?

Question

I am tring to selec two points A, B on the sphere (x-2)^2 + (y-4)^2 + (z-6)^2 ==9^2 so that EuclideanDistance[pA,pB] is an integer and coordinates of two point A, B are integer numbers. I know that, with distance AB= 12, I tried

ClearAll[a, b, r, c];
{a, b, c} = {2, 4, 6};
 r = 9; ss = 
 Subsets[{x, y, z} /. 
   Solve[{(x \[Minus] a)^2 + (y \[Minus] b)^2 + (z \[Minus] c)^2 == 
      r^2, x y z != 0}, {x, y, z}, Integers], {2}];
mydistance = Select[ss, EuclideanDistance[#[[1]], #[[2]]] == 12 &];
Select[mydistance, (6 == Length[Union @@ #] &)]

{{{-7, 4, 6}, {1, -4, 2}}, {{-7, 4, 6}, {1, -4, 10}}, {{-7, 4, 6}, {1, 8, -2}}, {{-7, 4, 6}, {1, 8, 14}}, {{-7, 4, 6}, {1, 12, 2}}, {{-7, 4, 6}, {1, 12, 10}}, {{-6, 3, 2}, {-2, 11, 10}}, {{-6, 3, 10}, {-2, 11, 2}}, {{-6, 3, 10}, {2, -5, 6}}, {{-6, 5, 2}, {-2, -3, 10}}, {{-6, 5, 10}, {-2, -3, 2}}, {{-6, 5, 10}, {2, 13, 6}}, {{-6, 8, 5}, {2, 4, -3}}, {{-6, 8, 7}, {2, 4, 15}}, {{-5, 8, 2}, {3, 12, 10}}, {{-5, 8, 10}, {3, 12, 2}}, {{-2, -4, 5}, {2, 4, -3}}, {{-2, -4, 7}, {2, 4, 15}}, {{-2, -3, 10}, {6, 5, 14}}, {{-2, 3, 14}, {2, -5, 6}}, {{-2, 3, 14}, {6, 11, 10}}, {{-2, 5, 14}, {2, 13, 6}}, {{-2, 5, 14}, {6, -3, 10}}, {{-2, 8, -1}, {6, 12, 7}}, {{-2, 8, 13}, {6, 12, 5}}, {{-2, 11, 10}, {6, 3, 14}}, {{-2, 12, 5}, {2, 4, -3}}, {{-2, 12, 5}, {6, 8, 13}}, {{-2, 12, 7}, {2, 4, 15}}, {{-2, 12, 7}, {6, 8, -1}}, {{1, 12, 2}, {9, 8, 10}}, {{1, 12, 10}, {9, 8, 2}}, {{2, 4, -3}, {6, -4, 5}}, {{2, 4, -3}, {6, 12, 5}}, {{2, 4, -3}, {10, 8, 5}}, {{2, 4, 15}, {6, -4, 7}}, {{2, 4, 15}, {6, 12, 7}}, {{2, 4, 15}, {10, 8, 7}}, {{3, -4, 2}, {11, 4, 6}}, {{3, -4, 10}, {11, 4, 6}}, {{3, 8, -2}, {11, 4, 6}}, {{3, 8, 14}, {11, 4, 6}}, {{3, 12, 2}, {11, 4, 6}}, {{3, 12, 10}, {11, 4, 6}}}

I want to find all integert numbers that EuclideanDistance[pA, pB] == k. I tried

ClearAll[a, b, r, c];
    {a, b, c} = {2, 4, 6};
     r = 9; ss = 
     Subsets[{x, y, z} /. 
       Solve[{(x \[Minus] a)^2 + (y \[Minus] b)^2 + (z \[Minus] c)^2 == 
          r^2, x y z != 0}, {x, y, z}, Integers], {2}];
    Table[{pA, pB} = points;
     Solve[{EuclideanDistance[pA, pB] == k, 1 <= k <= 2 r}, k, Integers],
     {points, ss}]

{{}, {}, {}, {}, {}, {}, {{k -> 6}}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 12}}, {{k -> 12}}, {{k -> 12}}, {{k -> 12}}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {{k -> 8}}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 6}}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 16}}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 6}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 16}}, {{k -> 18}}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 12}}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {{k -> 16}}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {{k -> 16}}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 18}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k
-> 8}}, {}, {}, {}, {{k -> 12}}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {{k -> 16}}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 8}}, {}, {}, {{k -> 18}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k
-> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 8}}, {{k -> 18}}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {{k -> 18}}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 18}}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {{k -> 8}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {{k -> 12}}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {{k -> 18}}, {{k -> 6}}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {{k -> 6}}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {{k -> 6}}, {{k -> 12}}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 12}}, {{k -> 12}}, {}, {}, {}, {}, {}, {{k -> 18}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {{k -> 12}}, {}, {}, {{k -> 6}}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 12}}, {}, {}, {}, {{k -> 8}}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {{k -> 12}}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 8}}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k
-> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {{k -> 16}}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {{k -> 6}}, {}, {}, {}, {{k -> 16}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k
-> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {{k -> 14}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{{k -> 12}}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {{k -> 6}}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 12}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {}, {},
{}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {}, {}, {}, {}, {}, {}, {{k -> 6}}, {{k -> 8}}, {{k -> 2}}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}, {}, {{k -> 8}}, {}, {}, {}, {}, {}, {}, {{k -> 2}}, {}, {}}

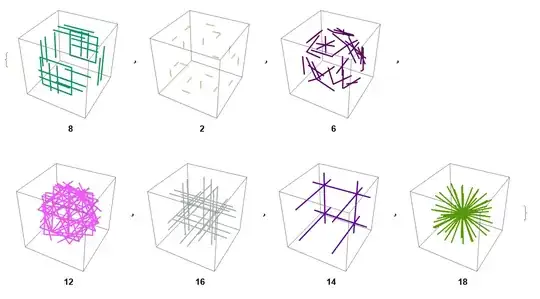
From this out put, I see that, $k \in \{2, 6, 8, 12, 14, 16, 18\}$. How to get a nice Ouput?

Answer 1

This

ClearAll[x1,x2,y1,y2,z1,z2,d];
a=2;b=4;c=6;r=9;
sol={x1,y1,z1,x2,y2,z2,d}/. FindInstance[
  (x1-a)^2+(y1-b)^2+(z1-c)^2==r^2&&
  (x2-a)^2+(y2-b)^2+(z2-c)^2==r^2&&
  (x1-x2)^2+(y1-y2)^2+(z1-z2)^2==d^2&&d>0,
  {x1,y1,z1,x2,y2,z2,d},Integers,10^3];
goodsol=Select[sol,Length[Union[Take[#,6]]]==6&]
Map[Last,goodsol]

My apologies for my misunderstanding. So you don't want a distance of 12, any distance will do, but you do want distinct integers. Hopefully this is right now.

So that returns 308 solutions.

If all you want to know are the distances between the points then that last line of code will discard the points and leave the distance between them.

Please tell me if I have made any other mistakes. I am still not sure that I've really captured exactly what you are trying to do. Could you perhaps add a carefully chosen long sentence, perhaps starting from the title that you used, but describe exactly any and all conditions that you want to hold? Or perhaps you could explain why you didn't just change the 12 in the original code with k and add k to the list of things to solve for. Maybe that would make it clear. Thanks

Try

{a,b,c}={2,4,6};r=9;
ss=Subsets[{x,y,z}/.Solve[{(x-a)^2+(y-b)^2+(z-c)^2==r^2,x y z!=0}, 
  {x,y,z},Integers],{2}];
goodss=Select[ss,IntegerQ[Norm[#[[1]]-#[[2]]]]&]
dist=Map[Norm[#[[1]]-#[[2]]]&,goodss]
Union[dist]

which will show you all the satisfactory points, all the distances and then just the short list of unique distances

Answer 2

{a, b, c} = {2, 4, 6};
r = 9;
pts = SolveValues[{(x - a)^2 + (y - b)^2 + (z - c)^2 == r^2, 
    x y z != 0}, {x, y, z}, Integers];
list = Flatten[
   Table[If[
     i > j && 
      IntegerQ[EuclideanDistance[pts[[i]], pts[[j]]]], {pts[[i]], 
      pts[[j]], EuclideanDistance[pts[[i]], pts[[j]]]}, Nothing], {i, 
     Length@pts}, {j, Length@pts}], 1];
groups = GatherBy[list, Last];
Graphics3D[{AbsoluteThickness[2], RandomColor[], Line@#}] & /@ 
 groups[[;; , ;; , 1 ;; 2]]