A simpler or more concise way to divide the boundary of a polygon into equal arc lengths?

Question

I am really looking just for the least amount of code needed to do this but it is still readable.

Here is the same polygon but the border is respectively split up into 10, 20, and 30 points along the perimeter:

The code I used to produce this is:

OrderVerticesClockwise[pts_List] := Module[
  {pivot, sorted, remainingPoints},
(* Find the pivot: the lowest and leftmost point *)
  pivot = First[SortBy[pts, {Last, First}]];
(* Remove the pivot from the list *)
  remainingPoints = DeleteCases[pts, pivot];
(* Sort the remaining vertices based on the polar angle relative to the pivot *)
  sorted = SortBy[remainingPoints, ArcTan[#[[1]] - pivot[[1]], #[[2]] - pivot[[2]]] &];
(* Return ordered vertices with the pivot at the beginning *)
  Prepend[sorted, pivot]
]
Clear[EquidistantPoints];
EquidistantPoints[pts_List, n_Integer] := Module[
  {
    closedPts = Append[pts, First[pts]],
    lengths, totalLength, interval, accumulatedLengths, currentPt, nextPt,
    distRemaining, currentIndex, result = {}
  },
lengths = EuclideanDistance @@@ Partition[closedPts, 2, 1];
  totalLength = Total[lengths];
  interval = totalLength/n;
accumulatedLengths = Accumulate[lengths];
Do[
    distRemaining = i*interval;
    currentIndex = 1;
While[distRemaining &gt; accumulatedLengths[[currentIndex]],
  currentIndex++;
];

distRemaining -= If[currentIndex &gt; 1, accumulatedLengths[[currentIndex - 1]], 0];

currentPt = closedPts[[currentIndex]];
nextPt = closedPts[[currentIndex + 1]];

AppendTo[result, currentPt + (distRemaining/lengths[[currentIndex]]) * (nextPt - currentPt)];

, {i, 0, n - 1}

];
result
]
equiArcLengthPointQuantity=20;
poly = RandomPolygon[12];
vertices = PolygonCoordinates[poly];
orderedVertices = OrderVerticesClockwise[vertices];
equiArcDistances = Accumulate[Table[Perimeter[poly]/equiArcLengthPointQuantity, {i, 1, equiArcLengthPointQuantity}]];
equidistantPts = EquidistantPoints[orderedVertices, equiArcLengthPointQuantity];
Graphics[
  {Polygon[orderedVertices], Red, PointSize[0.02], Point[equidistantPts]}
]

I would assume that there is a much simpler way of doing this, but I couldn't think of one. And I don't know what else to call these points. They aren't equally distanced points in Euclidean space, just along the perimeter by arc length.

cvgmt · Accepted Answer · 2023-08-30T00:16:19.153

8

MeshFunctions -> {"ArcLength"} partly work.

poly = RandomPolygon[10];
plot=ListLinePlot[Append[#, First@#] &@poly[[1]], 
 MeshFunctions -> {0 &, "ArcLength"}, Mesh -> {Subdivide@10}, 
 MeshStyle -> Red, Epilog -> {Opacity[.2], poly}, Axes -> False]

pts =Cases[plot // Normal, Point[p_] :> p, -1] // DeleteDuplicates

edited Aug 30 '23 at 00:16

answered Aug 29 '23 at 05:53

cvgmt

72,231
4
75
133

1

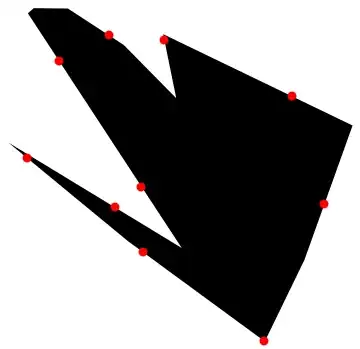
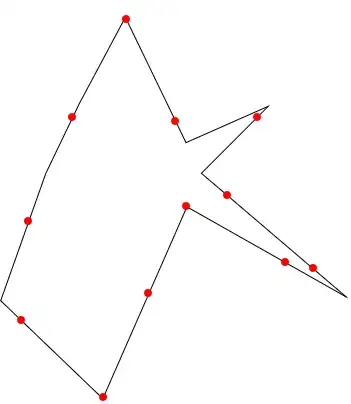
Where did you find "ArcLength" for MeshFunctions? MeshFunctions -> {0 &, "ArcLength" – Daniel Huber Aug 29 '23 at 09:25
3

@DanielHuber The setting 0& come from https://mathematica.stackexchange.com/a/277682/72111 The MeshFunctions of "ArcLength" is well know in this forum. – cvgmt Aug 29 '23 at 11:17
1

ArcLength seems not always to give equidistant points. E.g.: Plot[Sin[x ], {x, 0, 10}, MeshFunctions -> {0 &, ArcLength}, Mesh -> {10}, MeshStyle -> {PointSize[0.03]}] Do you know where to find info anout this? – Daniel Huber Aug 29 '23 at 11:44
1

@DanielHuber Mesh -> {10} will ignore the boundary points. So we need to use Mesh->{Subdivide@10} etc. – cvgmt Aug 29 '23 at 11:46
1

The points are still not equidistant. Where did you find info about "ArcLength"? – Daniel Huber Aug 29 '23 at 11:54
2

@DanielHuber This points are equidistant. For example, Plot[Sin[x], {x, 0, π*3}, MeshFunctions -> {0 &, "ArcLength"}, Mesh -> {{0, 0.5, 1}}, MeshStyle -> {PointSize[0.03]}] or Plot[Sin[x], {x, 0, π*3}, MeshFunctions -> {0 &, "ArcLength"}, Mesh -> {Subdivide[0, 1, 6]}, MeshStyle -> {PointSize[0.03]}] – cvgmt Aug 29 '23 at 12:01
1

You are right, I integrated it. It only looks optical different. – Daniel Huber Aug 29 '23 at 12:10
@cvgmt pts is always empty when I run it. – Teg Louis Aug 29 '23 at 23:00
1

@TegLouis Updated for old version, for example v12.3.1( I am using v13.3.1) – cvgmt Aug 30 '23 at 00:17
@cvgmt It completely works now. I use Google Chromebook, so I have to use the wolframcloud.com version. – Teg Louis Aug 30 '23 at 00:22

score 4 · Answer 2 · answered Aug 29 '23 at 09:47

We first create the points of a random polygon:

m = 10 ; (* polygon *)
pts = CirclePoints[m];
pts = RandomReal[{0.1, 2}] # & /@ pts;
AppendTo[pts, pts[[1]]];

Then we calculate the lines and their lengths of the border:

border = Partition[pts, 2, 1];
dist = Total[Norm[Subtract @@ #] & /@ border]/n;

Finally we distribute the points along the perimeter:

n = 12;(* number of points *)
rest = 0;
pts1 = Reap[Sow[pts[[1]]];
    Scan[(tmp = #[[1]];
       While[rest + Norm[#[[2]] - tmp] >= dist,
        Sow[
         tmp = tmp + (dist - rest)/Norm[#[[2]] - tmp] (#[[2]] - tmp)];
         rest = 0;];
       rest = Norm[#[[2]] - tmp]) &, border]
    ][[2, 1]];
Graphics[{Line[pts], Red, PointSize[0.03], Point[pts1]}]

kirma · Answer 3 · 2023-08-29T16:50:20.253

My primary tool is Interpolation:

 With[{poly = RandomPolygon[10], n = 50},
  With[{len = ArcLength@RegionBoundary@poly},
   (* Get a sequence of line segments. *)
   Partition[MeshPrimitives[poly, 2][[1, 1]] // Append[#, First@#] &, 
      2, 1, 1] //
     (* Create a linear constant-speed interpolation
        through polygon vertices. *)
     Interpolation[
       Transpose[
        {Accumulate[
          Prepend[EuclideanDistance @@@ Most@#, 0]], #[[All, 1]]}],
       InterpolationOrder -> 1] & //
    (* Generate points at constant intervals. *)
    Table[#[t], {t, 0, ((n - 1)/n) len, len/n}] &] // 
  Graphics[{poly, Red, PointSize@Large, Point@#}] &]

With poly = N@RegularPolygon[{1, 0}, 1000], n = 12:

By replacing two last lines of code with this you get an animation:

Animate[Graphics[{poly, Red, PointSize@Large, Point@#[t]}], {t, 0, len}] &

kglr · Answer 4 · 2023-09-01T17:59:44.990

Needs["GraphUtilities`"];

LSC[pts_, divs_] := Map[LineScaledCoordinate[pts, N @ #] &] @ Subdivide[divs]

Examples:

SeedRandom[1];
poly = RandomPolygon[10];
Graphics[{ Red , AbsolutePointSize[7], 
  Point[LSC[Append[#, First @ #] & @ poly[[1]], 10]], 
  EdgeForm[Gray], Opacity[.1], poly}]

Replace LSC[Append[#, First @ #] & @ poly[[1]], 10] with LSC[Append[#, First @ #] & @ poly[[1]], 5] to get

Plot[x Sin[3 x], {x, 0, 2 Pi}, 
 Filling -> Axis, 
 FillingStyle -> {LightRed, LightBlue},
 DisplayFunction -> 
  (Show[#, Epilog -> {Red, PointSize @ Large, 
     Point[First @ Cases[Normal@#, Line[x_] :> LSC[x, 7], All]]}] &)]

A simpler or more concise way to divide the boundary of a polygon into equal arc lengths?

4 Answers4