Why don't my Fourier series coefficients match with the output of the Discrete Fourier Transform (DFT)?

Question

The question I am about to ask should be more inclined towards a mathematical problem rather than Mathematica's syntax or application issues. However, I try to ask here first because I have received a lot of help here before.

My question is as follows: We can use DFT to calculate the spectrum, which can serve as an approximation of the Fourier series(FS) coefficients of a periodic function. Theoretically, the error of this approximation is known as aliasing error.

So I plan to verify this conclusion using Mathematica, to see how good the approximation is. The code and results will be presented at the end. When I take the periodic function as 4+3sin(t)+5sin(4t), the results of DFT and FS perfectly coincide. However, when I choose the periodic function as a square wave, the shapes of the output curves for both methods resemble sinc functions, but they do not match up. I have checked the code repeatedly but have not found any issues with it. I have tried increasing the number of discrete points, but it did not change the mismatch situation. I have also calculated using the relationship between FS and DFT coefficients, and the results match up...... I don't know where the problem lies.

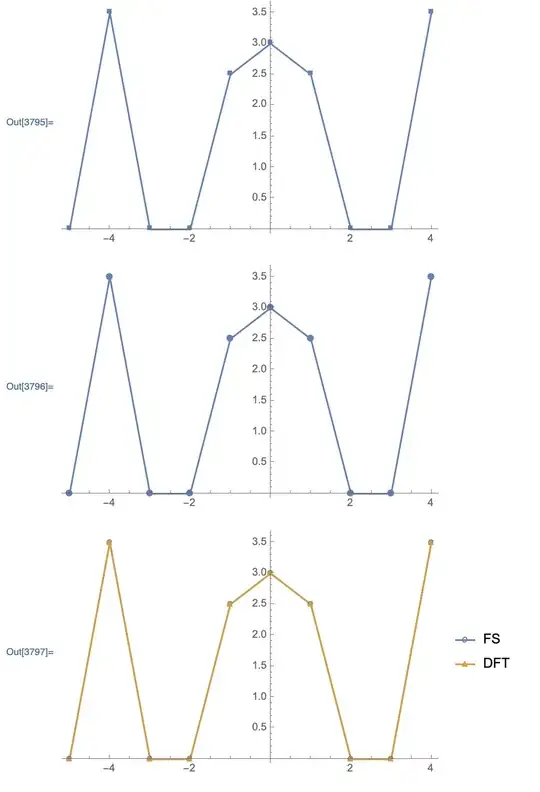
test 1: 3 + 5Sin[t] + 7Sin[4t]

Clear["Global`*"]
(* FS *)
f = 3 + 5Sin[t] + 7Sin[4t];
T = 2[Pi];
cn[nk_]:= FourierCoefficient[f,t,nk,FourierParameters->{1,(2[Pi])/T}];
(* DFT )
n = 10;
tlist = T/nRange[0,n-1];
flist = f/.t->tlist;
dftlist = Fourier[flist,FourierParameters->{-1, -1}];
shiftklist = (2[Pi])/T*Range[-Floor[n/2],-Floor[n/2]+n-1]; 
shiftdftlist = RotateRight[dftlist, Floor[Length[dftlist]/2]];
(* plot *)
cnlist = Table[cn[nk],{nk,-Floor[n/2],-Floor[n/2]+n-1}];
ListPlot[Transpose[{shiftklist,Abs@cnlist}],Joined->True,PlotMarkers->"[FilledSquare]"]
ListPlot[Transpose[{shiftklist,Abs@shiftdftlist}],Joined->True,PlotMarkers->"[FilledCircle]"]
ListPlot[
{ 
  Transpose[{shiftklist,Abs@cnlist}] ,
  Transpose[{shiftklist,Abs@shiftdftlist}] 
}
,Joined->True,PlotMarkers->{"o","[FilledUpTriangle]"},PlotRange->Full
,PlotLegends->{"FS","DFT"}]

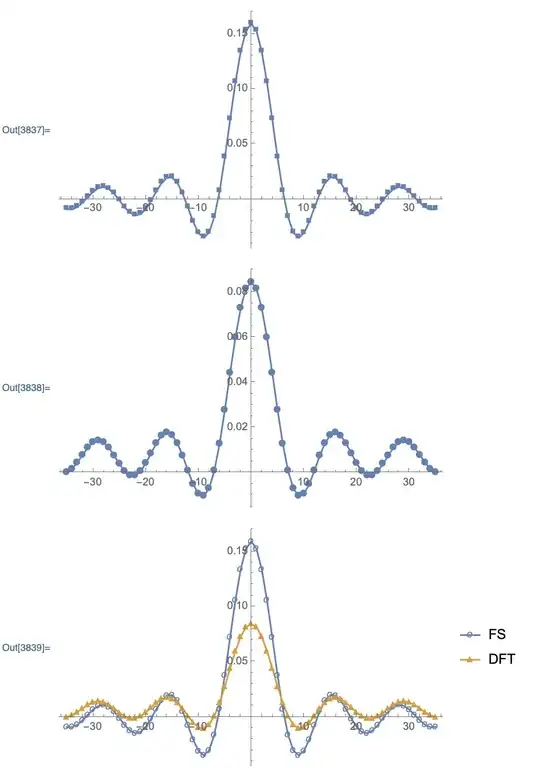
test 2: UnitBox[t]

Clear["Global`*"]
(* FS *)
f = UnitBox[t];
T = 2[Pi];
cn[nk_]:= FourierCoefficient[f,t,nk,FourierParameters->{1,(2[Pi])/T}];
(* DFT )
n = 71;
tlist = T/nRange[0,n-1];
flist = f/.t->tlist;
dftlist = Fourier[flist,FourierParameters->{-1, -1}];
shiftklist = (2[Pi])/T*Range[-Floor[n/2],-Floor[n/2]+n-1]; 
shiftdftlist = RotateRight[dftlist, Floor[Length[dftlist]/2]];
(* plot *)
cnlist = Table[cn[nk],{nk,-Floor[n/2],-Floor[n/2]+n-1}];
ListPlot[Transpose[{shiftklist,Re@cnlist}],Joined->True,PlotMarkers->"[FilledSquare]",PlotRange->Full]
ListPlot[Transpose[{shiftklist,Re@shiftdftlist}],Joined->True,PlotMarkers->"[FilledCircle]",PlotRange->Full]
ListPlot[
{ 
  Transpose[{shiftklist,Re@cnlist}] ,
  Transpose[{shiftklist,Re@shiftdftlist}] 
}
,Joined->True,PlotMarkers->{"o","[FilledUpTriangle]"},PlotRange->Full
,PlotLegends->{"FS","DFT"}]

Taking the first element of the list outputted by DFT as an example, theoretically, it should be equal to ...+Subscript[c, -2n]+Subscript[c, -n]+Subscript[c, 0]+Subscript[c, n]+Subscript[c, 2n]+..., so i do the sum in the following, The result matches well with the fundamental frequency coefficient of the Fourier series.

Sum[cn[nk],{nk,-100n,100n,n}] // N

---

@DanielHuber , i change the tlist and the code & pic is like following. Although the value matches, but only half, the other half is on the opposite axis. so strange & confused.

Clear["Global`*"]
(* FS *)
f = UnitBox[t];
T = 2[Pi];
cn[nk_]:= FourierCoefficient[f,t,nk,FourierParameters->{1,(2[Pi])/T}];
(* DFT )
n = 71;
(tlist = T/nRange[0,n-1];)
tlist = T/nRange[-Floor[n/2],-Floor[n/2]+n-1];
flist = f/.t->tlist;
dftlist = Fourier[flist,FourierParameters->{-1, -1}];
shiftklist = (2[Pi])/TRange[-Floor[n/2],-Floor[n/2]+n-1]; 
shiftdftlist = RotateRight[dftlist, Floor[Length[dftlist]/2]];
(* plot *)
cnlist = Table[cn[nk],{nk,-Floor[n/2],-Floor[n/2]+n-1}];
ListPlot[Transpose[{shiftklist,Re@cnlist}],Joined->True,PlotMarkers->"[FilledSquare]",PlotRange->Full]
ListPlot[Transpose[{shiftklist,Re@shiftdftlist}],Joined->True,PlotMarkers->"[FilledCircle]",PlotRange->Full]
ListPlot[
{ 
  Transpose[{shiftklist,Re@cnlist}] ,
  Transpose[{shiftklist,Re@shiftdftlist}] 
}
,Joined->True,PlotMarkers->{"o","[FilledUpTriangle]"},PlotRange->Full
,PlotLegends->{"FS","DFT"}]

---

one more test e^Sin[x], result: match

Clear["Global`*"]
(* FS *)
f = E^Sin[t];
T = 2[Pi];
cn[nk_]:= FourierCoefficient[f,t,nk,FourierParameters->{1,(2[Pi])/T}]
(* DFT )
n = 13;
tlist = T/nRange[0,n-1]; 
flist = f/.t->tlist;
dftlist = Fourier[flist,FourierParameters->{-1, -1}];
shiftklist = (2[Pi])/T*Range[-Floor[n/2],-Floor[n/2]+n-1]; 
shiftdftlist = RotateRight[dftlist, Floor[Length[dftlist]/2]];
(* plot *)
cnlist = Table[cn[nk],{nk,-Floor[n/2],-Floor[n/2]+n-1}];
ListPlot[Transpose[{shiftklist,Re@cnlist}]      ,Joined->True,PlotMarkers->"[FilledSquare]",PlotRange->Full]
ListPlot[Transpose[{shiftklist,Re@shiftdftlist}],Joined->True,PlotMarkers->"[FilledCircle]",PlotRange->Full]
ListPlot[
{ 
  Transpose[{shiftklist,Re@cnlist}] ,
  Transpose[{shiftklist,Re@shiftdftlist}] 
}
,Joined->True,PlotMarkers->{"o","[FilledUpTriangle]"},PlotRange->Full
,PlotLegends->{"FS","DFT"}]