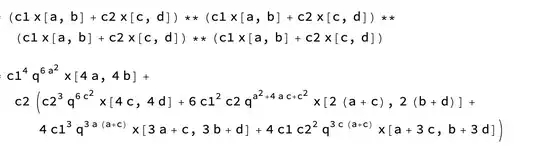How to define an infinite dimensional algebra with a known basis and multiplication rule?

Question

My goal is to do symbolic calculations in the noncommutative associative algebra generated by two elements $x,y$ satisfying the relation $x.y=q~y.x$. This infinite dimensional algebra has the basis $X_{i,j}=x^i y^j$ with multiplication rules $$X_{i,j}.X_{k,l}=q^{-jk}X_{i+k,j+l}.\tag{1}$$ I want to realize this multiplication rule as a function $m[A,B]$ where both $A$ and $B$ are (finite) linear combinations of $X_{i,j}$s and the output should also be linear combination of $X_{i,j}$s. How to do this in Mathematica?

Nothing in the current version supports this. Unless you find a package on the web, or someone willing to volunteer their time, you'll need to write this yourself. Start by writing down a detailed list of rules your new objects follow, then use some of the methods in the previous comment to implement these rules. — , Sep 04 '23 at 18:55
See section "Some noncommutative algebraic manipulation" in this conference talk from 1998. In particular there is an implementation of commutators. — Daniel Lichtblau, Sep 05 '23 at 23:51

score 2 · Accepted Answer · answered Sep 05 '23 at 06:35

2

rule=
    {
        x_**y_/;scalarQ[x]||scalarQ[y]:>x*y,
        (k_?scalarQ*x_)**y_:>k*x**y,
        x_**(k_?scalarQ*y_):>k*x**y,
        (x_+y_)**z_:>x**z+y**z,
        z_**(x_+y_):>z**x+z**y,
        x[i_,j_]**x[k_,l_]:>q^(i k) x[i+k,j+l]
    };

scalarQ[expr_]:=FreeQ[expr,x];

expr=NonCommutativeMultiply@@ConstantArray[(c1 x[a,b]+c2 x[c,d]),4]

expr//.rule//Simplify

answered Sep 05 '23 at 06:35

Lacia

2,253
3
19

Apart from a small typo in line 8 ($q^{i k}$ should actually be $q^{-jk}$), this solution works. – Lagrenge Sep 05 '23 at 19:05

Roland F · Answer 2 · 2023-09-05T19:14:07.083

A rather easy way of implementation is to use one of the different undefined product functions like CenterDot, CircleDot as containers and implement the axioms by patterns. This is just a proposal to be tested for functioning. Since TensorExpand does not work on CenterDot as with containers TensorProduct and Wedge, it has to be implemented explicitely.

     Protect[X,q];
   X/:  VectorQ[Subscript[X,_,_]]:=True
   q:/NumberQ[q]:=True
 QScalarQ[x__]:= FreeQ[Times[x],Subscript[X,_,_]]


(CenterDot as the algebra defining TensorProduct )
 QExpand={  CenterDot[a___,Subscript[X,i_,j_],Subscript[X,m_,n_],b___]] :&gt;
            Exp[- q j m]*CenterDot[a___,Subscript[X,i+m,j+n] ,b]  ,

(*The other rules are multilinearity with repect to + and scalar Times  *)

  (* Multilinearity for Plus  *)

  CenterDot[a___,b_Plus,c___]] :&gt; (CenterDot[a,#_,c]&amp;)/@b  ,

  (*  Scalar Times multilinearity *)

     CenterDot[a___,p__?QScalarQ *  Subscript[X,i_,j_] ,b___]] :&gt; 
      Times[p]* CenterDot[a,Subscript[X,i,j] ,b]    }

    CenterDot[] :=1
    CenterDot[x_]:=x

Use it by

expr //.QExpand

How to define an infinite dimensional algebra with a known basis and multiplication rule?

2 Answers2