Artifacts when interpolating on an unstructured set of 3D data

Question

When doing an interpolation on an unstructured set of points it is best to use the interpolation method available from the finite element package. However, it is essential that some re-scaling is done so that a good mesh can be achieved. I have hit this problem before and this is a continuation of the problem I discussed here.

I now have the problem of reversing the scaling so that I can have an interpolation function in the true values. I can do this but artifacts appear on the boundary due to unwanted extrapolation. Can these be avoided or at least removed?

I start by making some points and values to go with the points

pts = Table[t {100 Cos[t], Sin[t]}, {t, 0, 100, 0.1}];
values = {#[[1]], #[[2]], #[[1]] #[[2]]^2} & /@ pts;
pa = Graphics3D[Point[values], BoxRatios -> {1, 1, 1}, Axes -> True, 
  AxesLabel -> {"x", "y", "z"}]

Note that the scaling on the x and y axes differ by a factor of 100.

The next step is to re-scale make the mesh and an interpolation function on the mesh. This works as follows

        Needs["NDSolve`FEM`"];
{x1, x2} = MinMax[pts[[All, 1]]];
{y1, y2} = MinMax[pts[[All, 2]]];
pts1 = {Rescale[#[[1]], {x1, x2}, {-1, 1}], 
     Rescale[#[[2]], {y1, y2}, {-1, 1}]} & /@ pts;
mesh = ToElementMesh[pts1];
int = ElementMeshInterpolation[{mesh}, values[[All, 3]],
   "ExtrapolationHandler" -> {Function[Indeterminate], 
     "WarningMessage" -> False}];
Plot3D[int[x, y], {x, y} \[Element] mesh, BoxRatios -> {1, 1, 1}]

This is all very satisfactory but my axes are scaled between -1 to 1. To un-scale I have made a function that maps the un-scaled data to the scaled data. This works but on plotting there are artifacts on the boundary.

ClearAll[fint];
fint[x_, y_] := 
  int[-1 + 2 (x - x1)/(x2 - x1), -1 + 2 (y - y1)/(y2 - y1)];
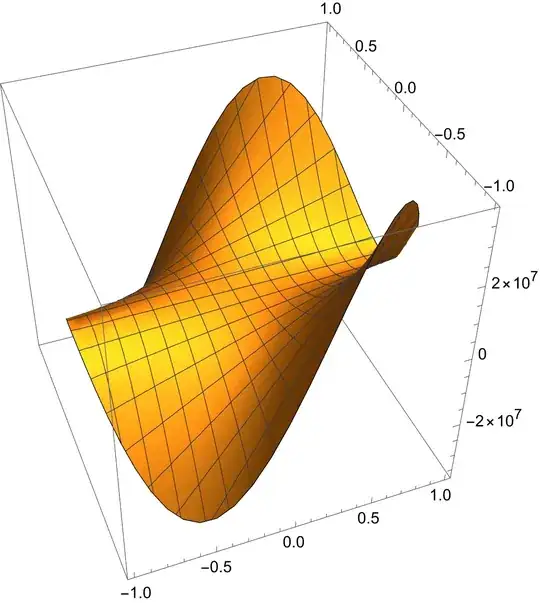
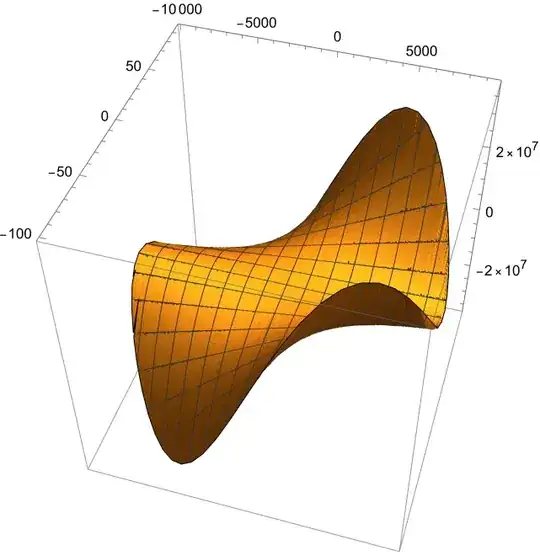
Plot3D[fint[x, y], {x, -10000, 10000}, {y, -100, 100}, 
 PlotPoints -> {100, 100},
 BoxRatios -> {1, 1, 1}]

Can the artifacts be removed? Perhaps I am being too fussy but I am also concerned that if I use the interpolation function then I could get false outputs.

Edit

Henrik Schumacher asks "Why do you rescale at all?

If we don't rescale then this is the mesh we get

mesh = ToElementMesh[pts];
Show[mesh["Wireframe"], AspectRatio -> 1]

This is clearly hopeless and I think it may be the reason why ListPlot3D does not work. Thus

ListPlot3D[values, BoxRatios -> {1, 1, 1}, PlotRange -> All]

Why do you rescale at all? Apparently, the rescaling leads to tiny errors for the boundary points so that some of them fall outside of the domain of interpolant. — Henrik Schumacher, Sep 15 '23 at 16:58
@HenrikSchumacher Please see edit which shows why it does not work — Hugh, Sep 16 '23 at 19:10
@user21 Could you explain more? For an irregular region I can't see how to use PlotRange — Hugh, Sep 16 '23 at 19:12
@Hugh Uh, oh. Thank you for the plot. Now I realize that object has very different size in the x- and y-direction (which makes problems with the mesh generation). — Henrik Schumacher, Sep 16 '23 at 22:30
try undoScaling[values] @ ListPlot3D[reScale @ values] using the functions undoScaling and reScale from this answer ? — kglr, Sep 17 '23 at 01:38
Another thing to try is to use an Automatic extrapolation handler — user21, Sep 17 '23 at 04:23

score 3 · Accepted Answer · answered Sep 17 '23 at 11:24

3

How about something like this:

m1 = ToElementMesh["Coordinates" -> pts];
ClearAll[fint];
fint[x_, y_] := 
  int[-1 + 2 (x - x1)/(x2 - x1), -1 + 2 (y - y1)/(y2 - y1)];
Plot3D[fint[x, y], {x, y} \[Element] m1, PlotPoints -> {100, 100}, 
 BoxRatios -> {1, 1, 1}]

answered Sep 17 '23 at 11:24

user21

39,710
8
110
167

A good and surprising answer. It seems that although you are using the bad mesh I show in the question this mesh works well as a definition of the region to be plotted. – Hugh Sep 17 '23 at 16:29
The solution from @kglr unscales the data in the plot. Is it possible to unscale the coordinates in the mesh? – Hugh Sep 17 '23 at 16:31
@Hugh, not that I can think of now. – user21 Sep 18 '23 at 13:23

Artifacts when interpolating on an unstructured set of 3D data

1 Answers1