How to find the zero crossings of a periodic function?

Question

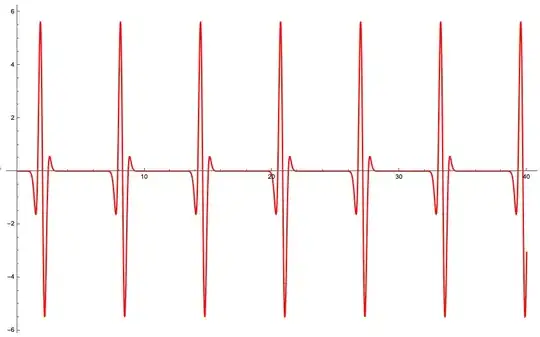
I have a function as follows,

$ \pi^{\prime}_{xx} = \exp(-2 k_x^2 \sin^2(\frac{t}{2})) k_x^2 \theta(t) \times \bigg[ -\frac{\sin(2t)}{2} - \cos(t) \sin(t) (1 - k_x^2 \sin^2(\frac{t}{2})) + 2 \cos(t) \sin^2(\frac{t}{2}) \sin^2(t) + 2 \sin^2(t)- 4 k_x^2 \sin^2(t) \sin^2(\frac{t}{2}) - 2 \sin(2t) \cos(t) \sin^2(t) - \sin(2t) \sin^2(t) + 2 k_x^2 \sin(2t) \sin^2(t) \sin^2(\frac{t}{2}) \bigg]$

I plotted it like

pixx = k^2 Exp[-2 k^2 Sin[(t)/2]^2 ](-Sin[2t] - Sin[t](1-k^2 Sin[t]^2));
piyy = k^2 Exp[ -2 k^2 Sin[(t)/2 ]^2 ](-4Sin[t]Sin[(t)/2]^2 - Sin[t](1-4k^2 Sin[(t)/2]^4)) ;
pixy = k^2 Exp[-2k^2 Sin[(t)/2 ]^2 ](2Cos[t]Sin[(t)/2]^2 + Sin[t]^2 - 2 k^2 Sin[(t)/2]^2 Sin[t]^2);
xxrot = Cos[t + 2.0 - [Pi] / 2]^2 pixx + 
   Sin[t + 2.0 - [Pi] / 2]^2 piyy - 
   Sin[2 (t + 2.0 - [Pi] / 2)] pixy;
i2k[i_] = 1/2 (i - 1) ;
xxrotplt = 
 Plot[  xxrot /. k -> -i2k@10 /. t -> t - 2 // Evaluate, {t, 0, 
   4000 0.01}, PlotRange -> All, PlotStyle -> Red];

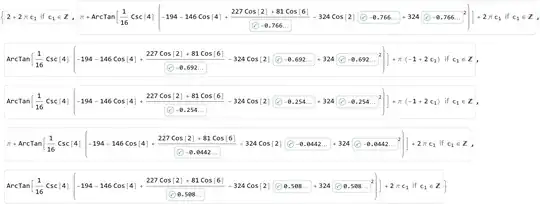
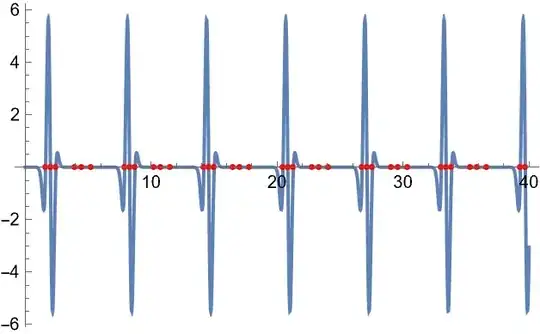
So I need to know in which values in x-axis I have the zero crossings of the function as accurately as possible.

I tried to make a table and use interpolation, but it obviously does not give accurate values.

Could use a method from this MSE post – Daniel Lichtblau Oct 10 '23 at 15:14 — Daniel Lichtblau, Oct 10 '23 at 15:14

score 4 · Accepted Answer · answered Oct 10 '23 at 11:35

4

g[t_] = (xxrot /. k -> -i2k@10 /. t -> t - 2 // Evaluate);

roots = t /. FindRoot[g[t], {t, #}] & /@ Range [0, 40, 0.1] // 
   Select[# < 40 &] // DeleteDuplicatesBy[Round[#, 10^-4] &]

Plot[g[t], {t, 0, 40}
 , PlotRange -> All
 , AspectRatio -> 1/3
 , Epilog -> {AbsolutePointSize[5], Red
   , Point@{#, 0} & /@ roots
   }
 ]

answered Oct 10 '23 at 11:35

Syed

52,495
4
30
85

+1 Much better than my answer, which I will delete – eldo Oct 10 '23 at 11:39

JimB · Answer 2 · 2023-10-11T14:58:16.307

There is an exact solution.

pixx = k^2 Exp[-2 k^2 Sin[(t)/2]^2] (-Sin[2 t] - Sin[t] (1 - k^2 Sin[t]^2));
piyy = k^2 Exp[-2 k^2 Sin[(t)/2]^2] (-4 Sin[t] Sin[(t)/2]^2 - Sin[t] (1 - 4 k^2 Sin[(t)/2]^4));
pixy = k^2 Exp[-2 k^2 Sin[(t)/2]^2] (2 Cos[t] Sin[(t)/2]^2 + Sin[t]^2 - 2 k^2 Sin[(t)/2]^2 Sin[t]^2);
xxrot = Cos[t + 2 - \[Pi]/2]^2 pixx + Sin[t + 2 - \[Pi]/2]^2 piyy - Sin[2 (t + 2 - \[Pi]/2)] pixy;
i2k[i_] = 1/2 (i - 1);
f = xxrot /. k -> -i2k@10 /. t -> t - 2 // Evaluate // FullSimplify
(* 81/64 E^(81/4 (-1 + Cos[2 - t])) (146 Sin[4] - 81 Sin[2 - 3 t] + 
   162 Sin[4 - 2 t] - 292 Sin[2 - t] - 81 Sin[6 - t] - 162 Sin[2 t] + 16 Sin[2 + t]) *)

So we see that 81/64 E^(81/4 (-1 + Cos[2 - t])) can't be zero so the solutions are found with

sol = (t /. Solve[(146 Sin[4] - 81 Sin[2 - 3 t] + 162 Sin[4 - 2 t] - 292 Sin[2 - t] - 
81 Sin[6 - t] - 162 Sin[2 t] + 16 Sin[2 + t]) == 0, t]) // FullSimplify

To obtain a table of all solutions to 20 significant digits where k is any integer:

sol = (sol //. ArcTan[r_] :> N[ArcTan[r], 20]) // Expand;
sol //. C[1] -> k;
sol[[3]] = sol[[3]] + N[2 \[Pi], 20];
sol[[4]] = sol[[4]] + N[2 \[Pi], 20];
sol[[6]] = sol[[6]] + N[2 \[Pi], 20];
(sol = (List @@@ sol)[[All, 1]] /. C[1] -> k // Sort) // TableForm

score 2 · Answer 3 · answered Oct 10 '23 at 12:22

2

expr = xxrot /. k -> -i2k@10 /. t -> t - 2
NSolve[{expr == 0, 0 <= t <= 4000 0.01}, t]

answered Oct 10 '23 at 12:22

cvgmt

72,231
4
75
133

score 1 · Answer 4 · answered Oct 10 '23 at 21:03

xxrotplt = 
 Plot[xxrot /. k -> -i2k@10 /. t -> t - 2 // Evaluate, {t, 0, 40}, 
  PlotRange -> All, Mesh -> {{0}}, MeshFunctions -> { #2 & }, 
  MeshStyle -> Directive[PointSize[0.01], Red]]

FindRoot[xxrot /. k -> -i2k@10 /. t -> t - 2 // Evaluate, {t, #}] & /@
    Cases[Normal@xxrotplt, Point[{t_, _}] -> t, \[Infinity]] // Sort // DeleteDuplicates

{{t -> 1.61503}, {t -> 2.}, {t -> 2.44387}, {t -> 3.94832}, {t -> 4.45579}, {t -> 5.24495}, {t -> 7.89822}, {t -> 8.28319}, {t -> 8.72705}, {t -> 10.2315}, {t -> 10.739}, {t -> 11.5281}, {t -> 14.1814}, {t -> 14.5664}, {t -> 15.0102}, {t -> 16.5147}, {t -> 17.0222}, {t -> 17.8113}, {t -> 20.4646}, {t -> 20.8496}, {t -> 21.2934}, {t -> 22.7979}, {t -> 23.3053}, {t -> 24.0945}, {t -> 26.7478}, {t -> 27.1327}, {t -> 27.5766}, {t -> 29.0811}, {t -> 29.5885}, {t -> 30.3777}, {t -> 33.031}, {t -> 33.4159}, {t -> 33.8598}, {t -> 35.3642}, {t -> 35.8717}, {t -> 36.6609}, {t -> 39.3141}, {t -> 39.6991}}

How to find the zero crossings of a periodic function?

4 Answers4