my equation is:
k[a_?NumericQ, b_?NumericQ, c_?NumericQ] := NDSolve[{r^3 b x''[r] y[r] - 12 x[r] y[r] -
4 r^3 b y''[r] x[r] == 0, 4 (2 x'[r]^2 +
2 x[r]x''[r])/Sqrt[c] + (2 y'[r]^2 +
2 y[r] y''[r])/Sqrt[c] == -4b/r,x[1] == 0, y[1] == Sqrt[-4 b Log[2/b]/(c^(-1/2))],
y'[1] == c^(1/4) (-4 b - 4 b Log[2 /b])/(2 Sqrt[-4 b Log[2/b] ] ), x'[1] == a},
{x, y}, {r, 1, b/2}, MaxSteps -> 1000000]
and then I plot it:
Plot[Evaluate[{x[r], y[r]} /. k[1, 50, 10^(-7)]], {r, 1, 25}]
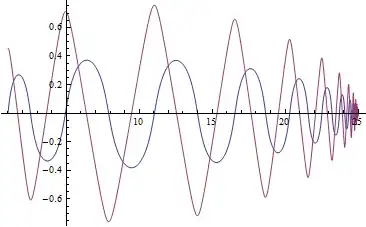
this one is okay, cause x[r] and y[r] both equal to 0 at r=b/2
if I set a=0 and the other parameters stay the same

I do not know how comes this sigularity at r=b/2, basing on the second equation in NDSolve, 4 (2 x'[r]^2 +
2 x[r]x''[r])/Sqrt[c] + (2 y'[r]^2 +
2 y[r] y''[r])/Sqrt[c] == -4b/r comes from the second derivative of r in this equation:
c^(-1/2) 4 x[r]^2 + c^(-1/2) y[r]^2 == -4 r b Log[(2 r)/b]
so it's easy to check, if x[r]=0 all the way, y[r] should be 0 at r=b/2
does anyone know how to resolve the infinity at r=b/2 for any values of the parameter?
a>=0, b>2, 10^(-3)>c>10^(-7)
thanks a lot

WorkingPrecisionthat isn't high enough. There're numbers of posts aboutWorkingPrecisionin this site, e.g. this, you can have a search for more details. – xzczd Jul 26 '13 at 14:26