13

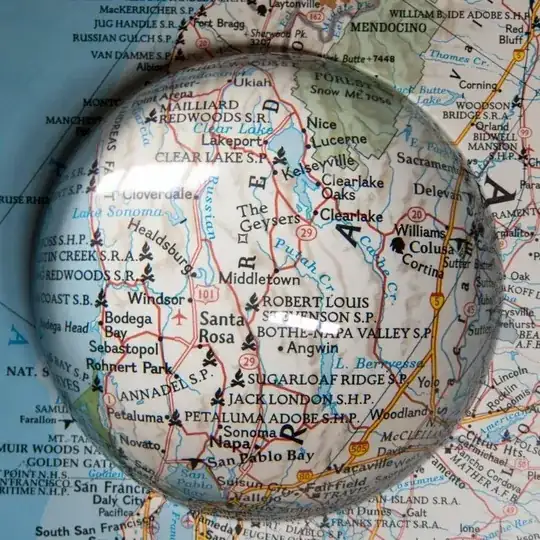
UPDATE: Code from this post was used for video generation here: Cinematically moving a lens over images: magnifying glass effect in videos

enter image description here

I am trying to create a magnifying glass effect for images with small text and other features similar to realistic one you can see above. My basic solution is based on an example I saw in docs on ImageTransformation - see Fish Eye effect in Neat Examples section.

MG[img_, radius_, pos_, strength_] := Module[
  {transform},
  transform[pt_] := With[
    {
      r = Norm[pt - pos],  (* Distance from the center of the magnifying glass *)
      a = ArcTan @@ (pt - pos)  (* Angle with respect to the center *)
    },
    If[
      r < radius,  (* If the point is inside the magnifying glass *)
      pos + (r/strength) {Cos[a], Sin[a]},  (* Apply the magnifying effect *)
      pt  (* Otherwise, keep the point unchanged *)
    ]
  ];
  (* Highlight the boundary of the magnifying glass using a black circle *)
  HighlightImage[ImageTransformation[img, transform, 
  DataRange -> Full, Padding -> White], {Gray, Circle[pos, radius]}]
];

Lets get some test image:

testIMG=ImageResize[Rasterize[StringTake[
ExampleData[{"Text","DeclarationOfIndependence"}],5000]],800]

And test:

MG[testIMG, 150, {200, 200}, 2]

enter image description here

But it is far from good imitation of realistic optical effect. Specifically, nice "flow" features from the page and into the glass at tis edges is not recreated. Please post your versions, that can be totally different or improvements - the goal is to get best effect close to optical one. No need to imitate reflectional glaring. The arguments of the function should be at least those I used taking image and lens position, size, and magnification strength.

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355

1 Answers1

14

In your code you use constant strength: (r/strength).

You can change it to depend on r:

linearly

r/((1 - strength)/radius r + strength)

or non-linearly

r/(1 + (Sqrt[radius^2 - r^2] (-1 + strength))/radius)

I used strength=2 for the images.

For linear dependence:

enter image description here

For non-linear dependence:

enter image description here

The non-linear dependence is more realistic.

Here is another version of non-linlinear dependence that is I think even better:

r/((1/(2 (-1 + strength)))(-1 - radius^2 + 
    Sqrt[(radius^2 + (-1 + strength)^2)^2 - 4 r^2 (-1 + strength)^2] +
     strength^2))

enter image description here

Here are depicted dependences of strength s on radius r for strength=2 and radius=5, the first blue is linear, second orange is ellipsoidal and third green is circular.

enter image description here

azerbajdzan
  • 15,863
  • 1
  • 16
  • 48
  • Wow pretty cool improvement, thank you. How did you get these formulas, especially last one? – Vitaliy Kaurov Oct 19 '23 at 15:15
  • 1
    Simply - the curve must contain points {0,strength} and {radius, 1} (see black dots on my last image), because you want at center when r=0 strength to be strength and at border of the radius when r=radius strength 1. Strength 1 means no magnification at all. – azerbajdzan Oct 19 '23 at 15:49
  • BTW i think it'd be cool to have publish this at the The Wolfram Function Repository – Vitaliy Kaurov Nov 03 '23 at 06:35
  • @Vitaliy Kaurov: If you know how to publish there then do so. I have not published there anything and do not know how to do it. – azerbajdzan Nov 04 '23 at 20:11
  • It is easy. Less complicated than publishing on this forum. I prefer original authors to publish it because it counts as a publication. Let me know if you'd like to email about the details. – Vitaliy Kaurov Nov 05 '23 at 05:05