Visualizing conformal map from upper half plane to n-gon

Question

I want to plot both the upper half plane and the image of it i.e. a polygonal region via Schwarz-Christoffel maps. One example is for a quadrilateral.

 f[z_]:= Integrate[1/((z - z1)^a1  (z - z2)^a2  (z - z3)^a3  
  (z - z4)^a4 ),z]

where a1+a2+a3+a4 = 2 and say, z1 = 1, z2 = 2, z3 = 5, z4 = 7.

Eventually I want to plot more complicated cases, e.g. polygon with circular arcs (hyperbolic polygons)

Edit : I am trying to use the known map from upper half plane to triangle with all three angles vanishing i.e. F[z] = EllipticK[z]/EllipticK[1-z]

What I get doesn't look like a triangle to me. Here is what I tried.

 F[z_] := EllipticK[z]/EllipticK[1 - z]
 data = RandomComplex[{-200, 200 + 400 I}, 10^6];
 uhp = ComplexListPlot[data];
 polygon = ComplexListPlot[F[data]];
 GraphicsRow[{uhp, polygon}]

A bit relevant https://mathematica.stackexchange.com/a/111521/9469 — yarchik, Jan 18 '24 at 21:20

score 2 · Answer 1 · answered Jan 19 '24 at 22:06

Realize than you are mapping only points in a tiny rectangular portion of infinite upper half plane {-200, 200 + 400 I} so the points can not be spread over the whole area of a triangle. And also the density of points that is even on half plane would not be even on the triangle.

I do not know where the function F[z] = EllipticK[z]/EllipticK[1-z] came from and what triangle it should represent (spherical, hyperbolic, Euclidean) but I assume it is correct (have not checked that).

From Schwarz_triangle_function I took this definition of Euclidean triangle mapping to compare with OP function.

(*function fu[z] from wiki*)
a = (1 - α - β - γ)/2;
b = (1 - α + β - γ)/2;
c = 1 - α;
aa = a - c + 1;
bb = b - c + 1;
cc = 2 - c;
fu[z_] := 
 z^α Hypergeometric2F1[aa, bb, cc, z]/
    Hypergeometric2F1[a, b, c, z] /. 
   z -> z /. {α -> 1/3, β -> 1/3, γ -> 1/3}
(OP's function F[z])
F[z_] := EllipticK[z]/EllipticK[1 - z]

Now OP's plots of both:

data = RandomComplex[{-10, 10 + 2*10 I}, 10^5];
uhp = ComplexListPlot[data];
polygon = ComplexListPlot[F[data], PlotRange -> {{0, 2}, {0, 2}}];
GraphicsRow[{uhp, polygon}]
polygon = 
  ComplexListPlot[fu[data], 
   PlotRange -> {{0.88331 - 1, 0.88331 + 1}, {-0.1, 1.6}}, 
   Epilog -> {Line[{{0, 0}, {1.7666387502854501, 0}, {0.88331, 
        1.52995403}, {0, 0}}]}];
GraphicsRow[{uhp, polygon}]

So we see mappings seems to be correct, although OP's mapping is not Euclidean triangle.

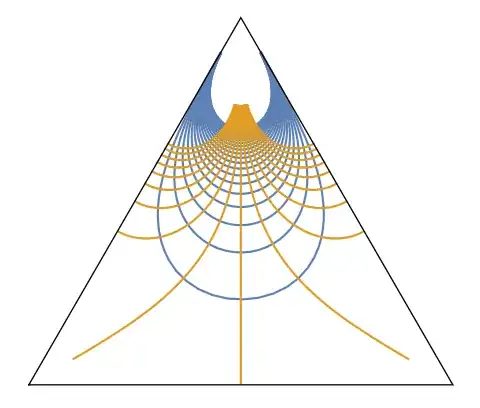
There is a better depiction of mappings (not by random points but) by grid lines. Here is such a depiction that uses the wiki's function fu[z].

ParametricPlot[
  Table[ReIm[fu[x + I y]], {y, 1/2, 10, 1/2}], {x, -200, 200}, 
  Frame -> False, Axes -> False, 
  Epilog -> {Line[{{0, 0}, {1.7666387502854501, 0}, {0.88331, 
       1.52995403}, {0, 0}}]}, 
  PlotRange -> {{0.88331 - 1, 0.88331 + 1}, {-0.1, 1.6}}];
ParametricPlot[
  Table[ReIm[fu[x + I y]], {x, -4, 5, 1/2}], {y, 0.01, 20}, 
  PlotStyle -> ColorData[97, 2], Frame -> False, Axes -> False];
Show[%%, %]

Could you help to see this post? When the polygon has more than three sides (like a pentagon), I don't know how to use the Schwarz-Christoffel map — yode, Jan 20 '24 at 03:47
@yode: In your question the red region is not a polygon so Schwarz–Christoffel mapping does not apply. — azerbajdzan, Jan 20 '24 at 10:09
Yeah, I know, so my idea is to discretize it into a polygon first. Doesn't Hollywood use triangles for circles? — yode, Jan 20 '24 at 10:45

Visualizing conformal map from upper half plane to n-gon

1 Answers1