How to produce a Calder mobile?

Question

Alexander Calder (1898 - 1976) was an American artist known for for his mobiles and his public sculptures.

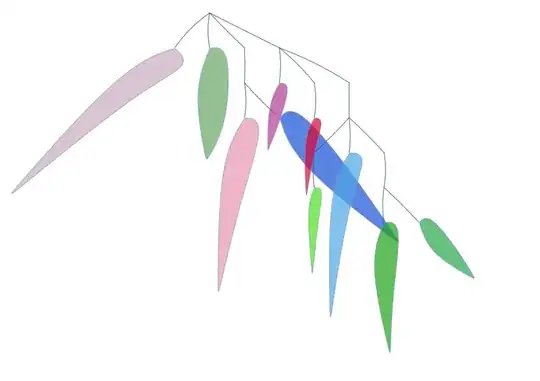
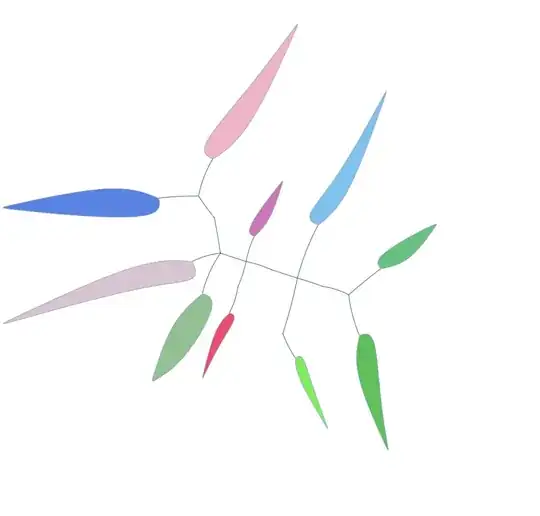
Here are two examples of his mobiles which I want to approximately reproduce with Mathematica:

The second example has different colors:

We can use BSplineCurve to draw a Calder-like rounded shape:

gr = Graphics[BSplineCurve[{{0, 0}, {1, 0}, {2.5, 0.5}, {1, 0.5}, {0, 1}}, SplineClosed -> True]]

and this answer of kglr: How to draw a colored curved shape to fill it:

BoundaryDiscretizeGraphics[gr, MeshCellStyle -> {2 -> Darker @ Red}]

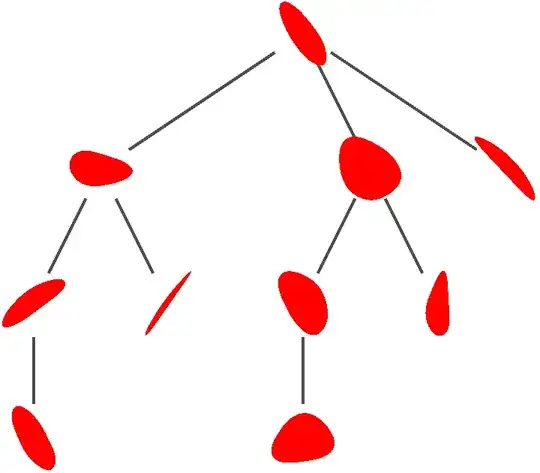
Maybe one could proceed with TreePlot, but with our rounded red shapes as VertexShapeFunction.

TreePlot[{1 -> 2, 2 -> 3, 3 -> 4, 4 -> 0, 5 -> 1, 6 -> 2, 7 -> 3, 8 -> 4, 9 -> 0},
 VertexShapeFunction -> "RoundedTriangle",
 VertexSize -> 0.2]

Or would it be easier to use Graphics- directives (slightly curved connected lines with randomized Calder-shapes)?

I don't know how to proceed and thank you in advance for any suggestions or, hopefully, a Calder-like solution.

So I suppose you also want these mobiles to be "physically" correct? Namely, when they are suspended, the forces and torques are in balance? :) — Domen, Nov 02 '23 at 10:20
Nope - I'm more interested in an aesthetically appealing image. — eldo, Nov 02 '23 at 10:23
@azerbajdzan From the Cambridge Dictionary: "mobile: a decoration or work of art that has many parts that move freely in the air, for example hanging from threads" — flinty, Nov 02 '23 at 11:40
@flinty: Yes, also a kinetic sculpture as I found on https://en.wikipedia.org/wiki/Mobile_(sculpture). — azerbajdzan, Nov 02 '23 at 11:43
I have been playing around with kirma's answer here and getting random polygons with smooth edges. I haven't really figured out how to label tree vertices yet though, and it doesn't look perfect. — ydd, Nov 02 '23 at 15:49
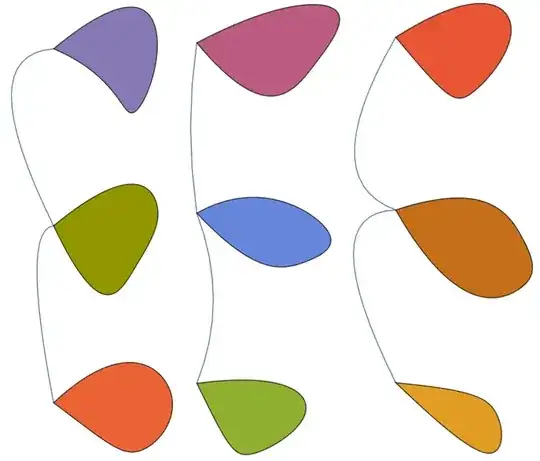
Something like ClusteringTree[RandomReal[1, 10]] could be a starting point. Maybe one can "extract" the tree-structure from there and "render" it as wanted? — Silvia, Nov 16 '23 at 18:04

score 3 · Answer 1 · answered Nov 02 '23 at 16:34

This answer is quite lacking, and there's a lot of improvements to be made. Maybe someone can improve on this however.

Using kirma's answer here (and modifying the parameters a little), we can get shapes (smoothed random polygons) that kind of look like Calder shapes.

We can then assign the VertexShapes to be these random smooth polygons:

SeedRandom[1234];
{minPolySides, maxPolySides} = {3, 6};
mobileStructure = {1 -> 2, 2 -> 3, 3 -> 4, 4 -> 0, 5 -> 1, 6 -> 2, 
   7 -> 3, 8 -> 4, 9 -> 0};
numberofThings = 10;
randomPolys = 
  Table[With[{coords = 
      Append[#, #[[1]]] &@
       RandomPolygon[{"Convex", 
          RandomInteger[{minPolySides, maxPolySides}]}][[1]]}, 
    With[{ip = 
       Interpolation[
        Transpose@{Rescale@
           Accumulate@
            Prepend[EuclideanDistance @@@ Partition[coords, 2, 1], 0],
           coords}, InterpolationOrder -> 1]}, 
     Graphics[{FaceForm@Red, 
       Polygon@Table[
         Mean@Table[ip[Mod[t + t0, 1]], {t0, 0, 0.3, .01}], {t, 0, 
          1., .01}]}]]], numberofThings];
vs = Thread[Range[0, numberofThings - 1] -> randomPolys];
TreePlot[mobileStructure,
 VertexShape -> vs, VertexSize -> 0.5, EdgeStyle -> Thick, 
 BaseStyle -> Black]

Mathematica graphics

This is still missing some critical properties of your two examples though:

It looks like in your examples of Calder's mobiles, some tree vertices do not have a "shape" on them, and are instead just branching points for multiple shapes to hang off of.
The shapes are really not perfect still, I think I may have made them too smooth

+1 - it's much more than just a promising start :) – eldo Nov 02 '23 at 16:40 — eldo, Nov 02 '23 at 16:40

kglr · Accepted Answer · 2023-11-02T20:52:57.993

With minor modifications of gr in OP:

ClearAll[randomLeaf]
randomLeaf  := Module[{tip = {RandomReal[{2, 5}], RandomReal[{-1/2, 0}]}}, 
  Graphics[
   BSplineCurve[{{0, 0}, {0, 0},  {1, -1/2}, tip, tip,
      {RandomReal[{1, 3}], RandomReal[{0, 1/3}]}, {0, 1/2}}, 
    SplineClosed -> True]]]
SeedRandom[1];
Row @ Table[Show[randomLeaf, ImageSize -> 200], 5]

We can use randomLeaf as custom arrowhead in a custom EdgeShapeFunction as follows:

ClearAll[calderESF]
calderESF[leaflist_, sizes_: {.05,.2},curvature_ : {-.2, .2}] := 
 {Arrowheads[{{If[MemberQ[leaflist, #2[[2]]], 
     RandomReal[sizes], 0], 1.,
     Show @ BoundaryDiscretizeGraphics[randomLeaf, 
       MeshCellStyle -> {2 -> RandomColor[]}]}}], 
   GraphComputation`GraphElementData["CurvedEdge", 
     "Curvature" -> RandomReal[curvature]][##]} &

Examples:

branches = 
  Map[Reverse]@{1 -> 2, 2 -> 3, 3 -> 4, 4 -> 0, 5 -> 1, 6 -> 2, 
    7 -> 3, 8 -> 4, 9 -> 0};
leaves = GraphComputation`SinkVertexList @ Graph @ branches;
SeedRandom[1];
Graph[branches, 
 PerformanceGoal -> "Quality", 
 EdgeShapeFunction -> calderESF[leaves],
 VertexSize -> 0,
 VertexShapeFunction -> None, 
 GraphLayout -> "LayeredDigraphEmbedding", 
 ImagePadding -> {{50, 50}, {100, 10}}]

SeedRandom[1];
branches2 = EdgeList@IndexGraph@RandomTree@20;
leaves2 = GraphComputation`SinkVertexList @ Graph @ branches2;
SeedRandom[444];
Graph[branches2, 
 PerformanceGoal -> "Quality", 
 EdgeShapeFunction -> calderESF[leaves2], 
 VertexSize -> 0,
 VertexShapeFunction -> None, 
 GraphLayout -> "LayeredDigraphEmbedding", 
 ImageSize -> 700, 
 ImagePadding -> {{220, 150}, {200, 10}}]

Replace "LayeredDigraphEmbedding" with "RadialEmbedding" and, ImagePadding -> ... with ImagePadding -> 200 to get

score 2 · Answer 3 · answered Nov 02 '23 at 20:15

Simple example that you can play with.

vf[{xc_, yc_}, name_, {w_, h_}] := 
 Module[{rr = RandomReal[{-1/4, 0}]}, 
  BoundaryDiscretizeGraphics[
   BSplineCurve[{xc, yc} + RotationMatrix[rr*\[Pi]] . # & /@ {{0, 
       0}, {RandomReal[{0.5, 1}], 
       RandomReal[{-1, 0}]}, {RandomReal[{1, 2}], 
       RandomReal[{-1, 0}]}, {RandomReal[{1, 2}], 
       RandomReal[{1, 0}]}, {RandomReal[{0.5, 1}], 
       RandomReal[{1, 0}]}, {0, 0}}], 
   MeshCellStyle -> {2 -> ColorData[97, RandomInteger[15]]}]]
ef[pts_List, e_] := 
 BSplineCurve[{pts[[1]], Mean[pts] + RandomReal[{-1, 1}, 2], pts[[2]]}]
Graph[{1 -> 2, 2 -> 3}, VertexCoordinates -> {{0, 0}, {0, 2}, {0, 4}},
  VertexShapeFunction -> 1 | 2 | 3 -> vf, 
 EdgeShapeFunction -> (# -> ef & /@ {1 -> 2, 2 -> 3})]

How to produce a Calder mobile?

3 Answers3