I'm looking for a more efficient way to generate an image with a large number of randomly coloured Gaussians. Here's the code I'm using:
Remove["Global`*"]
(* Don't care about underflow of Exp *)
SetSystemOptions["CheckMachineUnderflow" -> False];
(* The minimum allowable determinant of the covariance matrix *)
detminscale = 0.1;
(* Make an association with the gaussian parameters. Reject with a
gaussian with alpha value zero if det constraint is violated *)
MakeGaussian[c_, a_, μ, Σ] :=
If[Det[Σ] < detminscale || !
PositiveDefiniteMatrixQ[Σ],
<|"c" -> {0, 0, 0}, "a" -> 0.0, "μ" -> μ,
"Σi" -> IdentityMatrix[2]|>,
<|"c" -> Clip[c, {0, 1}], "a" -> Clip[a, {0, 1}], "μ" -> μ,
"Σi" -> Inverse[Σ]|>
]
(* Evaluates the gaussian on the WxH grid, returning a 2D grid of RGBA tuples )
cfEvalGaussian =
Compile[{{c, _Real, 1}, {a, _Real}, {m, _Real, 1}, {s, _Real, 2}, {w, _Integer}, {h, _Integer}},
Table[
Append[c,
aClip[With[{X = ({i, j} - m)}, Exp[-X.s.X]], {0, 1}]], {i, 1, h}, {j, 1, w}
], CompilationTarget -> "C"];
(* Evaluates the gaussian and converts to an RGBA image *)
EvalGaussian[g_, w_, h_] :=
Image[cfEvalGaussian[g["c"], g["a"], g["μ"],
g["Σi"], w, h], ColorSpace -> "RGB"]
(* We evaluate all gaussians in parallel, the quiet is to silence underflow warnings.
TODO: other kernels don't respect the CheckMachineUnderflow !? *)
EvaluateAllGaussians[gs_, w_, h_] :=
ParallelTable[Quiet@EvalGaussian[g, w, h], {g, gs}]
ComposeRGBA[i1_, i2_] := ImageCompose[Image[i1], Image[i2]]
(* Starting from black, compose all the gaussian images over each other *)
ComposeGaussians[gres_, w_, h_] :=
Fold[ComposeRGBA, ConstantArray[{0, 0, 0, 1}, {w, h}], gres]
And this is how I'm testing it:
(* Generates a random positive semi-definite matrix, rejects bad det scales *)
randomGOMtx[scaler_] := Module[{M},
Until[detminscale < Det[M],
M = RandomVariate[
GaussianOrthogonalMatrixDistribution[RandomReal[scaler], 2]]
];
Return[M]
]
(* Test 500 random colour gaussians at 1024x1024 resolution )
With[{dmax = 1024, n = 500},
colours = RandomReal[1, {n, 3}];
alphas = RandomReal[{0.2, 1}, n];
means = RandomReal[{1, dmax}, {n, 2}];
matrices = Table[randomGOMtx[dmax1.0], n];
gaussians =
MapThread[MakeGaussian, {colours, alphas, means, matrices}];
evals = EvaluateAllGaussians[gaussians, dmax, dmax];
ComposeGaussians[evals, dmax, dmax]
]
I am also looking to try out the 3D case too (with Image3D), but the 2D case takes 2 minutes to produce an image, and 3d is likely to be much slower.
Update: This is the 3D case and it's painfully slow. I've also improved the matrix generation by using rotation matrices.
MakeGaussian[c_, a_, μ_, Σi_] :=
<|"c" -> Clip[c, {0, 1}], "a" -> Clip[a, {0, 1}], "μ" -> μ,
"Σi" -> Σi|>
cfEvalGaussian =
Compile[{{c, _Real, 1}, {a, _Real}, {m, _Real, 1}, {s, _Real,
2}, {w, _Integer}, {h, _Integer}, {d, _Integer}},
Table[
Append[c,
a*Clip[With[{X = ({i, j, k} - m)}, Exp[-X . s . X]], {0,
1}]], {i, 1, h}, {j, 1, w}, {k, 1, d}
], CompilationTarget -> "C"];
EvalGaussian[g_, w_, h_, d_] :=
cfEvalGaussian[g["c"], g["a"], g["μ"], g["Σi"], w,
h, d]
EvaluateAllGaussians[gs_, w_, h_, d_] :=
ParallelTable[Quiet@EvalGaussian[g, w, h, d], {g, gs}]
cfComposeRGBA = Compile[{{i1, _Real, 4}, {i2, _Real, 4}},
With[{w = Length[i1], h = Length[i1[[1]]],
d = Length[i1[[1, 1]]]},
Table[
With[{c1 = i1[[i, j, k]], c2 = i2[[i, j, k]],
a = i2[[i, j, k, 4]]},
c2a + c1(1 - a)
], {i, w}, {j, h}, {k, d}]
], CompilationTarget -> "C"];
randomGOMtx[scaler_] :=
With[{P = RotationMatrix[{{1, 0, 0}, RandomPoint[Sphere[]]}]},
Inverse[P] . DiagonalMatrix[1/RandomReal[{.1, scaler}, 3]] . P]
With[{dmax = 256, n = 50},
colours = RandomReal[1, {n, 3}];
alphas = RandomReal[{0.2, 1}, n];
means = RandomReal[{1, dmax}, {n, 3}];
matrices = Table[randomGOMtx[dmax*2], n];
gaussians =
MapThread[MakeGaussian, {colours, alphas, means, matrices}];
evals = EvaluateAllGaussians[gaussians, dmax, dmax, dmax];
Image3D[ComposeGaussians[evals, dmax, dmax, dmax],
ColorSpace -> "RGB"]
]

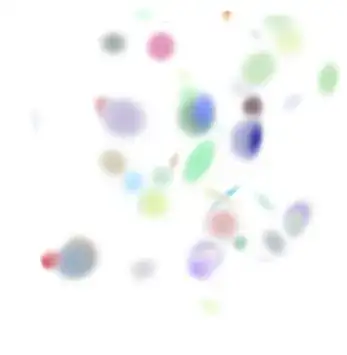






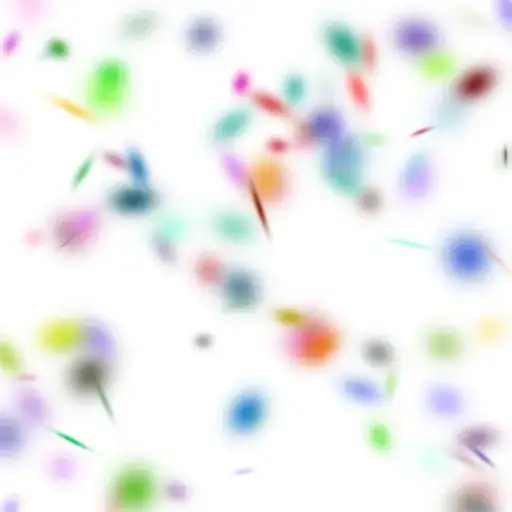
Needs["OpenCLLink`"]then runOpenCLQ[]and it crashes the kernel - doesn't even reply False. I've filed a bug report. – flinty Nov 06 '23 at 13:16OpenCLQ[]crashes the kernel because I had both the Intel oneAPI DPC C++ compiler installed and Visual Studio 2022. When I uninstalled the Intel one,OpenCLQ[]works and returns True! I informed Wolfram. – flinty Nov 07 '23 at 14:51