How to mesh a cylinder with helix points?

Question

I would like to mesh a cylinder surface. The mesh should include given cylinderpoints which lie on a helix.

My attempt using "IncludePoints"

zyl = ImplicitRegion[x^2 + y^2 == 1 && -Pi <= z <= Pi, {x, y, z}]
heli = ParametricRegion[{Cos[3 phi], Sin[3 phi],phi}, {{phi, -Pi, Pi}}]
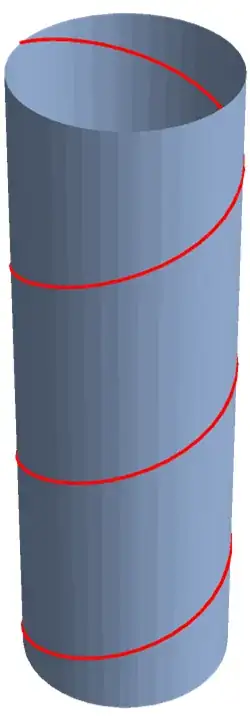
Show[{Region[zyl], Region[Style[heli, {Thickness[Large], Red}]] }]

some points of the helix

heliP = Map[#[[1]] &, MeshPrimitives[DiscretizeRegion[heli], 0] ];

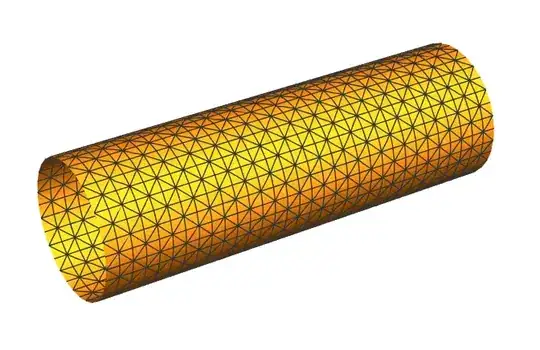
elementmesh

mesh = ToBoundaryMesh[zyl, "MeshElementType" -> "TriangleElement" , 
"MeshOrder" -> 1, "IncludePoints" -> heliP , "MaxCellMeasure" -> 1
]
Show[{mesh["Wireframe"], Graphics3D[{Red, Point[heliP]}]}]

Plot shows the complete triangle mesh, unfortunately the points of the helix(red) are no meshpoints!

What's wrong with my approach? Thanks!

IncludePionts is for full element meshes; more the include points can not be on the boundary. — user21, Nov 09 '23 at 00:08
@user21 Thanks for your comment. "Fullelement" mesh means space and element dimension must be the same? — Ulrich Neumann, Nov 09 '23 at 07:33
how does the option "MaxCellMeasure"->1 affect the outcome? @user21: the documentation says otherwise — wvt_beginner, Nov 09 '23 at 09:24
@user21 Simplified problem: How could I mesh a rectangle with constraint all included points of the diagonal are meshpoints (Mathematica v12.2)? Thanks! — Ulrich Neumann, Nov 09 '23 at 11:53
@UlrichNeumann, I'm not sure I understand you simplified question. You want to generate a boundary mesh and for that you need to give all cords and connectivity, To boundary mesh does not provide geometric operations such as splitting boundary elements. — user21, Nov 09 '23 at 16:30
@user21 Sorry if my comment is unclear. I would like to mesh(triangle) a Rectangle[] with the constraint that all meshpoints on the diagonal are predefined via "IncludePoints". — Ulrich Neumann, Nov 09 '23 at 16:40
@user21 ...and no elementside should cross the diagonal. The mesh should be a fullmesh in 2D — Ulrich Neumann, Nov 09 '23 at 16:45
IncludePoints works with ToElementMesh and not with ToBoundaryMesh. IncludePoints need to be inside the region and not in the boundary. — user21, Nov 09 '23 at 16:49
@UlrichNeumann, maybe something like addVertex from this q/a? — kglr, Nov 09 '23 at 20:52
@user21: https://reference.wolfram.com/language/FEMDocumentation/ref/ToBoundaryMesh.html at Option IncludePoints it is clearly written, that "These additional points are considered to be part of the boundary, but need not be on the actual boundary." — wvt_beginner, Nov 10 '23 at 10:08
@wvt_beginner, what that means is that all include points are addressable in, say, DirichletCondition but they can not be generated on the boundary. I'll clarify that statement in a future release. So it means that you can have a DirichletCondition (a boundary condition) inside the region. All points you want on the geometric boundary need to be specified through the coordinates and connectivity in ToBoundaryMesh — user21, Nov 10 '23 at 17:09
@wvt_beginner, I have clarified the documentation about the usage of "IncludePoints" This will be available in the 14.1 release (not in the imminent 14.0 release though). Thanks for pointing this out. I have other sections in the documentation that you feel are unclear, let me know and I'll see if I can improve them. Thx. — user21, Dec 06 '23 at 12:45

score 4 · Answer 1 · answered Nov 08 '23 at 23:13

4

Another method to achieve helical mesh.

m = 15;
ParametricPlot3D[{Cos[u], Sin[u], v}, {u, 0, 2 \[Pi]}, {v, 0, 
  2 \[Pi]}, MeshFunctions -> {#4 + #5 &}, Mesh -> 2 m + 1, 
 Boxed -> False, Axes -> False]
ParametricPlot3D[{Cos[u], Sin[u], v}, {u, 0, 2 \[Pi]}, {v, 0, 
  2 \[Pi]}, MeshFunctions -> {#4 + #5 &, #4 - #5 &}, Mesh -> 2 m + 1, 
 Boxed -> False, Axes -> False]
ParametricPlot3D[{Cos[u], Sin[u], v}, {u, 0, 2 \[Pi]}, {v, 0, 
  2 \[Pi]}, MeshFunctions -> {#4 + #5 &, #4 - #5 &, #4 &, #5 &}, 
 Mesh -> 2 m + 1, Boxed -> False, Axes -> False]

answered Nov 08 '23 at 23:13

azerbajdzan

15,863
1
16
48

1

The question is about generation an ElementMesh, how do you propose to move from your answer to that? – user21 Nov 09 '23 at 01:33
1

@user21: The OP original title/question: "How to mesh a cylinder with helix points?". That is what my answer provides - a helix mesh of a cylinder. – azerbajdzan Nov 09 '23 at 10:12
1

-1. This is a question and answer site not a title and answer site. So you read a title of a book and you know the content? – user21 Nov 09 '23 at 16:31

score 2 · Answer 2 · answered Nov 08 '23 at 19:54

2

       ParametricPlot3D[{40 Cos[ \[Phi]], 40 Sin[ \[Phi]], 
           z + 2.85 \[Phi] }, {\[Phi], 0, 2 \[Pi]}, {z, -100, 100}, 
                Mesh -> { 0, 10}, 
                    MeshStyle -> Directive[{ Red, Thickness[0.01]}], 
                  Boxed -> False]

answered Nov 08 '23 at 19:54

Roland F

3,534
1
2
10

1

Thanks for your effort, but I asked for a special meshing of a cylinder. – Ulrich Neumann Nov 08 '23 at 21:38

How to mesh a cylinder with helix points?

2 Answers2