0

I have a dataset following cosine function [e.g. cos(200t)] in time domain. In frequency domain two sharp lines should appear at -200 and +200. I have to do Fourier transform (or Fast Fourier transform) for that. I have tried the following code:

TDsignal = Table[{t, Cos[200 t]}, {t, 0, 1, 0.001}];
freq = Table[i/(Length[TDsignal[[All, 2]]] 0.001 ), {i, -((
           Length[TDsignal[[All, 2]]] - 1)/2), (
           Length[TDsignal[[All, 2]]] - 1)/2}];
FDdata = Transpose[{freq, Fourier[TDsignal[[All, 2]], FourierParameters -> {1, -1}]}];

Grid[{{ListLinePlot[TDsignal, PlotRange -> All, Axes -> False, 
         Frame -> True, FrameLabel -> {Style["time (s)", 12, FontFamily -> "Arial", 
         Bold], Style["TD signal  (au)", 12, FontFamily -> "Arial", 
         Bold]}, PlotStyle -> Hue[0.01, 0.43, 1.], AspectRatio -> 0.714,
         ImageSize -> 450], 
       ListLinePlot[Re@FDdata, PlotRange -> All, Axes -> False, 
          Frame -> True, FrameLabel -> {Style["Frequncy (Hz)", 12, FontFamily -> "Arial", 
          Bold], Style["FFT Signal  (au)", 12, FontFamily -> "Arial", 
          Bold]}, PlotStyle -> Hue[0.5, 0.43, 1.], AspectRatio -> 0.714, 
          ImageSize -> 450]}}]

It returns some lines but not at +/-200 (the plot what I got is attached here)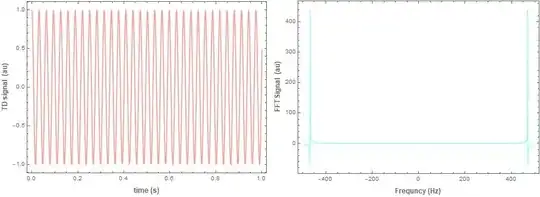enter image description here, but mathematically it must be at +/- 200. What is the mistake I am doing? Any lead will be really helpful.

P Pyne
  • 453
  • 2
  • 9
  • We really only care about the +ve frequency due to symmetry. I was going to post this but your question was deleted. here is screen shot Mathematica graphics – Nasser Nov 10 '23 at 13:02
  • Thank you for your help, but in your code you considered cos[2pi200*t]; so if we perform FourierTransform on this function will give us (piDiracDelta[-400pi + w] + piDiracDelta[400pi + w]). So, in the frequency domain the peak should appear at +/-400pi.. but from your code I got the peak at 200... I am struggling still with this problem.. @Nasser – P Pyne Nov 10 '23 at 15:47
  • But cos[2*pi*200*t]; has frequency of 200 HZ? The x-axis is in HZ, not radians per second or any other units. – Nasser Nov 10 '23 at 21:30
  • I used Cos[2*Pi*200*t] as the signal. This is not exactly what you had. I did this to make it more clear. You had Cos[200 t], so you just need to transform yours to same form if you want to use my code. – Nasser Nov 10 '23 at 21:35
  • Ok, thank you for the clarification. I forgot to take care of 2 pi term. Thank you. Its really useful. – P Pyne Nov 13 '23 at 09:49

0 Answers0