5

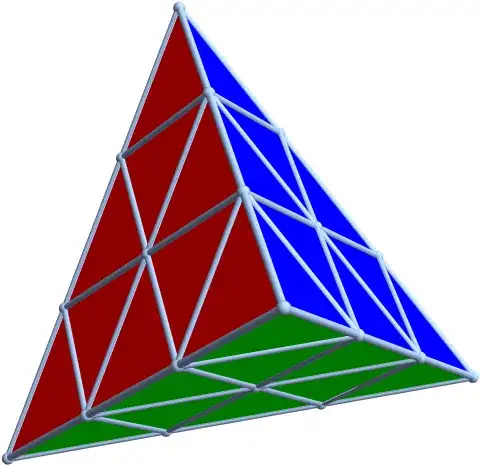
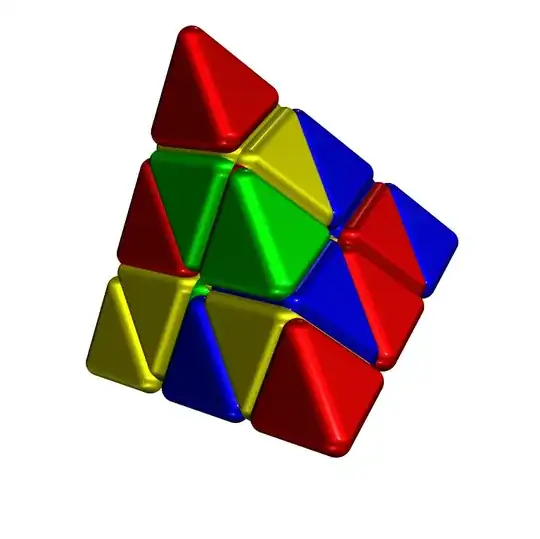
I want to draw to this picture. I am sorry, I do not know how to tell Mathematica do this. I do not know how to start.

enter image description here

Thuy Nguyen
  • 909
  • 4
  • 11

4 Answers4

13
dr = DiscretizeRegion[
      Tetrahedron[
       {{1, 0, -1/Sqrt[2]}, 
        {-1, 0, -1/Sqrt[2]}, 
        {0, -1, 1/Sqrt[2]}, 
        {0, 1, 1/Sqrt[2]}}], 
      MaxCellMeasure -> {"Length" -> Sqrt[3]/2}];

SeedRandom[1];

colors = Table[{2, i} -> FaceForm[RandomChoice[{Red, Yellow, Green, Blue}]], 
  {i, MeshCellCount[dr, 2]}];

MeshRegion[dr, 
 MeshCellStyle -> colors, 
 MeshCellShapeFunction -> 
  {1 -> (Tube[#1, .025] &), 
   0 -> (Sphere[#, 0.075] &)},
 Lighting -> "Neutral"]

enter image description here

facecolors = Join @@ MapThread[Thread @* Rule] @ 
  {Values @
    GroupBy[MeshCellIndex[dr, {2, "Boundary"}], 
       Round[Region`Mesh`MeshCellNormals[dr, #], 10^-5] &], 
   {Red, Blue, Yellow, Green}};

MeshRegion[dr, 
 MeshCellStyle -> facecolors, 
 MeshCellShapeFunction ->
  {1 -> (Tube[#1, .015] &), 
   0 -> (Sphere[#, 0.025] &)}, 
 Lighting -> "Neutral"]

enter image description here

dilationradius = 1/16;

mc3 = Map[
  RegionDilation[
     TransformedRegion[#, 
      ScalingTransform[1 - 5 dilationradius {1, 1, 1}, 
        RegionCentroid @ #]], 
    dilationradius] &] @
  MeshPrimitives[dr, 3];


SeedRandom[1];


Graphics3D[
 Map[{EdgeForm[], RandomChoice[
    MaterialShading[{"Glazed", #}] & /@ 
       {Red, Blue, Yellow, Green}], #} &] @ mc3, 
 Boxed -> False, ImageSize -> Large, Lighting -> "ThreePoint"]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
  • 1
    It is a Rubik's pyramid that cannot be solved. – azerbajdzan Nov 11 '23 at 15:57
  • @azerbajdzan, that's right. I changed the first version specifying polygon colors (replacing 3 with 2 in definition of colors), but ... it is too much work to specify face colors consistent with a rubik pyramid coloring scheme. – kglr Nov 11 '23 at 16:13
7
  • I don't know how to control the colors.
  • Here we use DiscretizeRegion to subdivide the Tetrahedron and use OpenCascadeLink to smooth the boundary.
Needs["OpenCascadeLink`"];
make[reg_] := 
 Module[{shape, fillet, bmesh, groups, g}, 
  shape = OpenCascadeShape[reg];
  fillet = OpenCascadeShapeFillet[shape, .015];
  bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[fillet];
   g = bmesh[
    "Wireframe"[
     "MeshElementStyle" -> (Directive@{EdgeForm[], 
           FaceForm[#]} & /@ {White, Yellow, Green})]]]
reg = Tetrahedron[PolyhedronData["Tetrahedron", "Points"][[;; , 1]]];
regs = MeshPrimitives[
   DiscretizeRegion[reg, MaxCellMeasure -> {"Length" -> Sqrt[3]/4}], 
   3];
make /@ regs // Show

enter image description here

cvgmt
  • 72,231
  • 4
  • 75
  • 133
4

As an example, we choose a Tetraeder with edge length= a.

We first construct only the bottom triangle. The vertex coordinates are:

a=1;
pts0 = pts = a  1/Sqrt[3] {{0, 1, 0}, {Sin[2 Pi/3], Cos[2 Pi/3], 
     0}, {Sin[-2 Pi/3], Cos[-2 Pi/3], 0}};

Now we add points to pts at 1/3 and 2/3 third of every edge:

pts = Function[x, (x[[1]] + #/3 (x[[2]] - x[[1]])) & /@ {0, 1, 2, 
      3}] /@ {pts[[1 ;; 2]], {pts[[3]], pts[[2]]}, {pts[[3]], 
     pts[[1]]}};

Next we add all the lines in the triangle:

lin = Line@Join[
    Transpose[{pts[[1, 1 ;; 3]], pts[[2, 1 ;; 3]]}],
    Transpose[{pts[[2, 2 ;; 4]], pts[[3, 2 ;; 4]]}],
    Transpose[{pts[[1, 2 ;; 4]], Reverse@pts[[3, 1 ;; 3]]}]
    ];

The coordinates of the top of the Tetraeder are:

 top = {0, 0, a Sqrt[2/3] };

We now have the bottom of the Tetraeder and we are going to rotate the bottom to get the sides. For this we need 3 rotations:

rt1 = RotationTransform[ArcTan[2 Sqrt[2]], pts0[[1]] - pts0[[2]], pts0[[1]]];
rt2 = RotationTransform[ArcTan[2 Sqrt[2]], pts0[[2]] - pts0[[3]], pts0[[2]]];
rt3 = RotationTransform[ArcTan[2 Sqrt[2]], pts0[[3]] - pts0[[1]], pts0[[3]]];

Now we have everything to draw the final picture:

Graphics3D[{Thickness[0.03], lin, GeometricTransformation[lin, rt1], 
  GeometricTransformation[lin, rt2], 
  GeometricTransformation[lin, rt3], Brown, Triangle[pts0], Yellow, 
  GeometricTransformation[Triangle[pts0], rt1], Red, 
  GeometricTransformation[Triangle[pts0], rt2], Blue, 
  GeometricTransformation[Triangle[pts0], rt3]}]

enter image description here

Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
4

Start with

 Graphics3D[{
  {EdgeForm[{Thick, Blue}], FaceForm[Green], 
   Tetrahedron[{0, 0, 0}]}, 
   {EdgeForm[{Thick, Orange}],FaceForm[Yellow], 
   Translate[Tetrahedron[{0, 0, 0}], {0.295, 0.485, 0.83}]}}, 
 Lighting -> "Neutral"]

enter image description here

Roland F
  • 3,534
  • 1
  • 2
  • 10