Solving PDE for Diffusion Equation (Boundary Condition Issue)

Question

I am trying to solve this partial diffusion equation shown

$$\dfrac{\partial\overset\sim\rho_c}{\partial\overset\sim t}=D_c(\overset\sim r)A\left(\dfrac{\partial^2\overset\sim\rho_c}{\partial\overset\sim r^2}+\dfrac2{\overset\sim r}\dfrac{\partial\overset\sim\rho_c}{\partial\overset\sim r}\right)$$

Dcoeff = 10^-29;
Rmax = 100*10^-6;
R = 10*10^-6;
eps = 0.1;
Cs = 1.0;
tmax = 1*10^21;
tref = 1;
A = Dcoeff*tmax/(Rmax^2)
sol = NDSolve[{D[Csol[r, t], t] == 
   A*(D[Csol[r, t], r, r] + (2/r) D[Csol[r, t], r]) + 
     NeumannValue[0, r == 0], Csol[r, 0] == 1, 
        DirichletCondition[Csol[r, t] == 0, r == 1]}, 
       Csol, {r, 0, 1}, {t, 0, tref}, 
       Method -> {MethodOfLines, 
         SpatialDiscretization -> {FiniteElement, 
           MeshOptions -> MaxCellMeasure -> 0.00001}}];
concentration[r_, t_] := Csol[r, t] /. sol[[1]];

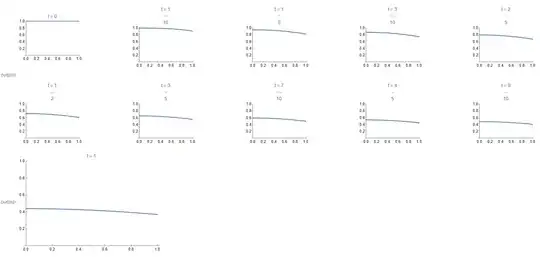
it evaluates fine, however when plotting seen in the image below, it does follow the dirichlet condition that states that r= 1 , the concentration = 0. I do hope a solution can be provided for this issue.

Grid[
 Partition[
  Table[Plot[Evaluate[concentration[r, t]], {r, 0, 1}, 
    PlotRange -> {0, 1}, FrameLabel -> {"r", "Concentration"}, 
    PlotLabel -> "t = " <> ToString[t]], {t, 0, tref, tref/10}], 5], 
 Spacings -> {10, 2}]
Plot[Evaluate[concentration[r, tref]], {r, 0, 1}, PlotRange -> {0, 1},
  FrameLabel -> {"r", "Concentration"}, 
 PlotLabel -> "t = " <> ToString[tref]]