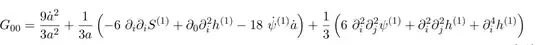I use the following MA code to calculate Einstein’s tensor. I’m asking about the zero component of the Einstein’s tensor, is it correct?
Because I think $G_{00}$ should contains the terms in the zero component of the metric , which is here $ g_{00} \sim \Phi[t,r,\theta,\phi]$
Also, as I will show although we make a linearization for the parameters in the metric:
( $\Phi, \Psi,S,\chi$ ) with respect to a factor n , fourth derivatives terms appear like $\chi^{(0, 0, 0, 4)} [t,r,\theta,\phi]$, so are these terms correct?
Here is the code:
x = {t, r, θ, ϕ};
met = a[t, y]^2*{{-(1 + 2*n*Φ[t, r, θ, ϕ]),
n*D[S[t, r, θ, ϕ], r],
n*D[S[t, r, θ, ϕ], θ],
n*D[S[t, r, θ, ϕ], ϕ]},
{n*D[S[t, r, θ, ϕ], r],
1 - 2*n*Ψ[t, r, θ, ϕ] +
n*D[Xi[t, r, θ, ϕ], {r, 2}] - (1/3)*n*
D[Xi[t, r, θ, ϕ], {θ, 2}] -
(1/3)*n*D[Xi[t, r, θ, ϕ], {ϕ, 2}],
n*D[D[Xi[t, r, θ, ϕ], r], θ],
n*D[D[Xi[t, r, θ, ϕ], r], ϕ]},
{n*D[S[t, r, θ, ϕ], θ],
n*D[D[Xi[t, r, θ, ϕ], r], θ],
1 - 2*n*Ψ[t, r, θ, ϕ] +
n*D[Xi[t, r, θ, ϕ], {θ, 2}] -
n*D[Xi[t, r, θ, ϕ], {r, 2}] - (1/3)*n*
D[Xi[t, r, θ, ϕ], {ϕ, 2}],
n*D[D[Xi[t, r, θ, ϕ], θ], ϕ]},
{n*D[S[t, r, θ, ϕ], ϕ],
n*D[D[Xi[t, r, θ, ϕ], r], ϕ],
n*D[D[Xi[t, r, θ, ϕ], θ], ϕ],
1 - 2*n*Ψ[t, r, θ, ϕ] +
n*D[Xi[t, r, θ, ϕ], {ϕ, 2}] - (1/3)*n*
D[Xi[t, r, θ, ϕ], {θ, 2}] -
(1/3)*n*D[Xi[t, r, θ, ϕ], {r, 2}]}};
metI := Inverse[met]
Chrest = ParallelTable[
Normal[Series[(1/2)*
Sum[metI[[i, p]]*(D[met[[p, j]], x[[k]]] +
D[met[[k, p]], x[[j]]] - D[met[[j, k]], x[[p]]]),
{p, 1, 4}], {n, 0, 1}]], {i, 1, 4}, {j, 1, 4}, {k, 1,
4}];
Reim = ParallelTable[
Normal[Series[
D[Chrest[[i, l, j]], x[[k]]] - D[Chrest[[i, k, j]], x[[l]]] +
Sum[Chrest[[i, k, m]]Chrest[[m, l, j]],
{m, 1, 4}] -
Sum[Chrest[[i, l, m]]Chrest[[m, k, j]], {m, 1, 4}], {n, 0,
1}]], {i, 1, 4}, {j, 1, 4}, {k, 1, 4}, {l, 1, 4}];
Ricci = ParallelTable[
Normal[Series[Sum[Reim[[m, i, m, j]], {m, 1, 4}], {n, 0, 1}]], {i,
1, 4}, {j, 1, 4}];
RScal = Normal[
Series[Sum[
Sum[metI[[i, j]]*Ricci[[i, j]], {i, 1, 4}], {j, 1, 4}], {n, 0,
1}]];
Eins = ParallelTable[
Normal[Series[
Ricci[[i, j]] - (1/2)met[[i, j]]RScal, {n, 0, 1}]], {i, 1,
4}, {j, 1, 4}]
Here is $G_{00}$ output
FullSimplify[Eins[[1, 1]]]
(1/3)((9Derivative[1, 0][a][t, y]^2)/a[t, y]^2 +
n(6Derivative[0, 0, 0, 2][Ψ][t,
r, θ, ϕ] +
Derivative[0, 0, 0, 4][Xi][t, r, θ, ϕ] +
6Derivative[0, 0, 2, 0][Ψ][t,
r, θ, ϕ] +
Derivative[0, 0, 2, 2][Xi][t, r, θ, ϕ] +
Derivative[0, 0, 4, 0][Xi][t, r, θ, ϕ] +
6Derivative[0, 2, 0, 0][Ψ][t,
r, θ, ϕ] +
2Derivative[0, 2, 0, 2][Xi][t, r, θ, ϕ] +
Derivative[0, 2, 2, 0][Xi][t, r, θ, ϕ] +
2Derivative[0, 4, 0, 0][Xi][t, r, θ, ϕ]) +
(1/a[t, y])(n Derivative[1, 0][a][t,y](-6Derivative[0, 0, 0, 2][S][t, r, θ, ϕ] - 6Derivative[0, 0, 2, 0][S][t, r, θ, ϕ] -
6Derivative[0, 2, 0, 0][S][t, r, θ, ϕ] -
18*Derivative[1, 0, 0, 0][Ψ][t, r, θ, ϕ] +
Derivative[1, 0, 0, 2][Xi][t, r, θ, ϕ] +
Derivative[1, 0, 2, 0][Xi][t, r, θ, ϕ] -
Derivative[1, 2, 0, 0][Xi][t, r, θ, ϕ])))
$G_{00}$ In Tex format:
I expects to be there $\Phi$ in the first term of $\dot{a}^2/a^2$. The metric in Tex form: