- For a curve we try to construct a polygon as its dilation.
- For such polygon we use
WindingPolygon with "TwoRule" to find its self intersection parts.
- After that we use
WhenEvent to look for the time which the line go through such region.
ρ[t_] = {6 Cos[t] - 3 Cos[6 t], 6 Sin[t] - 3 Sin[6 t]};
plot = ParametricPlot[ρ[t] +
s*Normalize[
RotationMatrix[π/2] . ρ'[t], # . #/Sqrt[# . #] &], {t,
0, 2 π}, {s, -1, 1}, PlotStyle -> None, PlotPoints -> 50,
MaxRecursion -> 2];
regs = WindingPolygon[
MeshPrimitives[DiscretizeGraphics@plot, 1][[;; , 1]][[;; , 1]],
"TwoRule"];
regs = MeshPrimitives[regs, 2];
dists = SignedRegionDistance /@ regs;
n = Length@regs;
fig[c_] :=
Module[{r, sols, pic, above, below},
r[t_] := ρ[t] +
c*Normalize[
RotationMatrix[π/2] . ρ'[t], # . #/Sqrt[# . #] &];
sols =
Table[Reap@
NDSolve[{z'[t] == r'[t], z[0] == r[0],
WhenEvent[dists[[i]]@z[t] == 0, Sow[t]]},
z, {t, 0, 2 π}], {i, 1, n}];
pic = Table[
ParametricPlot[z[t] /. sols[[1, 1, 1]], {t, 0, 2 π},
RegionFunction ->
Function[{x, y, t},
And @@ Table[! (sols[[i, 2, 1, 1]] <= t <= sols[[i, 2, 1, 2]] ||
sols[[i, 2, 1, 3]] <= t <= sols[[i, 2, 1, 4]]), {i, 1,
n}]]], {i, 1, n}];
above =
Table[ParametricPlot[z[t] /. sols[[1, 1, 1]], {t, 0, 2 π},
RegionFunction ->
Function[{x, y, t},
sols[[i, 2, 1, 1]] <= t <= sols[[i, 2, 1, 2]]]], {i, 1, n}];
below =
Table[ParametricPlot[z[t] /. sols[[1, 1, 1]], {t, 0, 2 π},
RegionFunction ->
Function[{x, y, t},
sols[[i, 2, 1, 3]] <= t <= sols[[i, 2, 1, 4]]]], {i, 1, n}];
{pic, above, below}]
choice = RandomChoice[{1, -1}, n]
Show[Table[{fig[c][[1,1]],
fig[c][[2]][[Position[choice, 1] // Flatten]],
fig[c][[3]][[Position[choice, -1] // Flatten]]}, {c,Subdivide[-.9, .9, 4]}],
Axes -> False, Frame -> False, PlotRange -> All]

- The above method work when the curve not so sharp and does not overlay so much.
Clear["Global`*"];
Charting`$InteractiveHighlighting = False;
pts = {{0, 0}, {1, 1}, {2, -1}, {3, 0}, {4, -2}, {6, 1}, {2, 3}, {2,
0}, {3, -2}, {4, -1}, {5, 2}, {4, 2}, {3, 2}, {1, 1}, {1, -1}};
ρ = BSplineFunction[pts];
L = .12;
s[t_] = ρ[t] +
c*Normalize[
RotationMatrix[π/2] . ρ'[t], # . #/Sqrt[# . #] &];
{a, b} = {0, 1};
plot = ParametricPlot[s[t], {t, a, b}, {c, -L, L}, PlotStyle -> None,
PlotPoints -> 60, MaxRecursion -> 2, PlotRange -> All];
regs = MeshPrimitives[
WindingPolygon[
MeshPrimitives[DiscretizeGraphics@plot, 1][[;; , 1]][[;; , 1]],
"TwoRule"], 2];
dists = SignedRegionDistance /@ regs;
n = Length@regs;
m = 5;
data = Table[
Reap@NDSolve[{z'[t] == s'[t], z[a] == s[a],
WhenEvent[dists[[i]]@z[t] == 0, Sow[t]]}, z, {t, a, b},
MaxStepSize -> 10^-3 L], {i, 1, n}, {c,
Subdivide[-.8 L, .8 L, m - 1]}];
fig0 = Show[
Table[ParametricPlot[
z[t] /. data[[1, j, 1]] // Evaluate, {t, 0, 1},
MeshStyle -> Transparent,
Mesh -> {Sort@Flatten@Table[data[[i, j, 2]], {i, 1, n}]},
MeshShading -> {Automatic, None}], {j, 1, m}], Axes -> False];
belt = ParametricPlot[s[t], {t, 0, 1}, {c, -.8 L, .8 L}, Mesh -> None,
PlotStyle -> Directive[Opacity[1], White], BoundaryStyle -> None,
PlotPoints -> 80, MaxRecursion -> 2];
trans = Table[
RandomChoice[{SubsetMap[Reverse, {2, 4}], Identity}], {i, 1, n}];
fig = Table[
ParametricPlot[z[t] /. data[[i, j, 1]] // Evaluate, {t, 0, 1},
Mesh -> data[[i, j, 2]], MeshStyle -> Transparent,
MeshShading ->
trans[[i]]@{None, Automatic, None, None, None}], {i, 1, n}, {j,
1, m}] // Show;
Show[belt, fig0, fig, Axes -> None, Frame -> None,
Background -> RGBColor[0.75, 0.3, 0.2]]

- We can use
Canvas[] to draw a line and extract the points from it by img[[1, 1]][[1 ;; -1 ;; 50]].
pts = {{-0.8833333333333332`,
0.6901204427083333`}, {-0.7785346137152778`,
0.8880995008680556`}, {-0.6285346137152777`,
0.8603217230902778`}, {-0.5313123914930555`,
0.6547661675347222`}, {-0.5368679470486111`,
0.3825439453125`}, {-0.48409016927083337`,
0.1964328342013888`}, {-0.3368679470486111`,
0.07421061197916656`}, {-0.20075683593750004`,
0.004766167534722143`}, {-0.04242350260416661`, \
-0.04801161024305567`}, {0.16313205295138888`, \
-0.08690049913194442`}, {0.3409098307291667`, -0.08412272135416665`}, \
{0.4825764973958333`, -0.12023383246527786`}, {0.6075764973958333`, \
-0.1952338324652778`}, {0.5659098307291668`, -0.4007893880208333`}, \
{0.5214653862847223`, -0.6896782769097223`}, {0.46868760850694446`, \
-0.9119004991319444`}, {0.3075764973958335`, -0.7813449435763888`}, \
{0.16868760850694442`, -0.7507893880208334`}, \
{-0.014645724826388928`, -0.7424560546875001`}, \
{-0.17853461371527768`, -0.720233832465278`}, {-0.27853461371527777`, \
-0.5924560546875`}, {-0.35909016927083326`, -0.40634494357638884`}, \
{-0.4924235026041667`, -0.2674560546875`}, {-0.6618679470486111`, \
-0.1424560546875`}, {-0.7202012803819444`, -0.2230116102430555`}, \
{-0.7007568359375`, -0.3646782769097223`}, {-0.6479790581597222`, \
-0.5146782769097222`}, {-0.6896457248263889`, -0.6369004991319445`}, \
{-0.6007568359375`, -0.720233832465278`}, {-0.4535346137152778`, \
-0.8146782769097225`}, {-0.311867947048611`, -0.8813449435763889`}, \
{-0.14797905815972223`, -0.6285671657986112`}, \
{-0.045201280381944375`, -0.47856716579861125`}, \
{0.06590983072916679`, -0.33412272135416665`}, {0.10202094184027777`, \
-0.13690049913194446`}, {0.12979871961805567`,
0.0714328342013888`}, {0.24646538628472237`,
0.20198838975694433`}, {0.39924316406250004`,
0.2492106119791666`}, {0.5409098307291667`,
0.19087727864583326`}, {0.5464653862847222`,
0.05198838975694442`}, {0.388132052951389`, \
-0.1785671657986112`}, {0.08257649739583339`, -0.27856716579861107`}, \
{-0.10909016927083326`, -0.1591227213541666`}, {-0.1424235026041667`,
0.15476616753472228`}, {-0.04797905815972214`,
0.4269883897569444`}, {-0.10353461371527772`,
0.5964328342013889`}, {-0.18686794704861098`,
0.7075439453125`}, {-0.028534613715277768`,
0.8214328342013889`}, {0.28257649739583335`,
0.7075439453125`}, {0.4547987196180556`,
0.5158772786458333`}, {0.635354275173611`,
0.49643283420138884`}, {0.6381320529513888`,
0.6492106119791666`}, {0.3492431640625`,
0.6103217230902778`}, {-0.08409016927083335`,
0.4714328342013888`}, {-0.4368679470486111`,
0.49643283420138884`}, {-0.6674235026041666`,
0.4380995008680555`}, {-0.7396457248263889`,
0.25476616753472214`}, {-0.6535346137152778`,
0.11032172309027777`}, {-0.4979790581597222`, \
-0.025789388020833304`}, {-0.4618679470486111`, \
-0.1869004991319445`}, {-0.6202012803819444`, -0.3507893880208335`}, \
{-0.8063123914930556`, -0.4563449435763889`}, {-0.8535346137152777`, \
-0.6035671657986112`}, {-0.7702012803819445`, -0.731344943576389`}, \
{-0.5313123914930555`, -0.6480116102430555`}, {-0.2757568359375`, \
-0.47856716579861125`}, {-0.09520128038194442`, \
-0.45078938802083335`}, {0.18257649739583348`, -0.4841227213541668`}, \
{0.5020209418402779`, -0.47856716579861125`}, {0.6909098307291668`, \
-0.35356716579861125`}, {0.7547987196180554`, -0.10912272135416679`}, \
{0.7492431640624999`, 0.15754394531250004`}, {0.6297987196180554`,
0.29087727864583335`}, {0.5103542751736112`,
0.28254394531249993`}, {0.4575764973958334`,
0.14921061197916674`}, {0.33535427517361116`,
0.03532172309027781`}, {0.2159098307291667`,
0.1325439453124999`}, {0.18813205295138902`,
0.4658772786458333`}, {0.1436876085069445`,
0.7130995008680555`}, {0.049243164062499956`,
0.8214328342013889`}, {-0.09520128038194442`,
0.8575439453125`}, {-0.2563123914930556`,
0.8408772786458334`}, {-0.43964572482638886`,
0.7436550564236111`}, {-0.6035346137152777`,
0.6214328342013888`}, {-0.7229790581597222`,
0.5880995008680555`}};
and set L = .035;, we get

pts = Table[{Cos[3 t], Sin[5 t]}, {t, Subdivide[0, .999*2 π, 50]}];
ρ = BSplineFunction[pts];
L = .035;














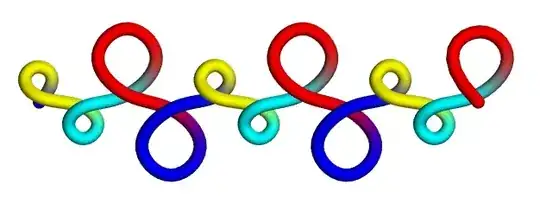



r {Cos[t], Sin[t]}.With[{r = 20, c = .2, ω = 10}, ParametricPlot[ r {Cos[t], Sin[t]} - c*r {Cos[ω*t], Sin[ω*t]}, {t, 0, 2 π}]]– cvgmt Nov 28 '23 at 01:10