Finding the general formula for the sequence defined by $u_1 = 1$ and $u_{n+1} = u_n + 1 + \sqrt{u_n+3}$

Question

Let be given sequence $(u_n)$ satisfying: $$u_1 = 1, \quad u_{n+1} = u_n + 1 + \sqrt{u_n+3}, \forall n \geq 1.$$ I tried

ClearAll["Global`*"];
RSolve[{a[x, n + 1] == a[x, n]  + 1 +  Sqrt[ a[x, n] + 3], 
  a[x, 1] == 1}, a[x, n], n]

{{a[x, n] -> 6 - 6 n + n^2}, {a[x, n] -> -2 + 2 n + n^2}}

With the answer a[x, n] -> -2 + 2 n + n^2}. I tried

Table[-2 + 2 n + n^2, {n, 10}]

{1, 6, 13, 22, 33, 46, 61, 78, 97, 118}

By hand, I get $u_2 = 1 + 1 + \sqrt{4} = 4. $

I also tried

RSolve[{a[n + 1] == a[n] + 1 + Sqrt[a[n] + 3], a[1] == 1}, a[n], n]

and get the same answer.

Where is wrong in my code to find $u_n$?

Answer 1

It could be that there is a closed form solution. Following considerations demonstrate that it cannot be simple. Important message is that $u_n$, besides quadratic grows demonstrated in the other answer, has sub-leading logarithmic terms.

Let us first reformulate the recurrence using the $t_n^2=u_n+3$ substitution. We get $$ t_{n+1}^2=t_n^2+t_n+1,\\ t_1=2. $$ MA cannot solve this recursion.

However, it can be reformulated introducing a difference $y_n=t_{n+1}-t_n$. We get $$ y_n(y_n+2t_n)=t_n+1. $$

This can approximately be written as an ordinary differential equation (ODE) $$ x'(t)\big(x'(t)+t\big)=t+1,\\ x(1)=2. $$

This can be solved analytically with MA

DSolve[{y'[x] (y'[x] + 2 y[x]) == y[x] + 1, y[1] == 2}, y[x], x]

we select the growing solution and define

f[x_] := 
 InverseFunction[-2 Log[-#1 + Sqrt[1 + #1 + #1^2]] + 
     3/2 Log[-1 - 2 #1 + 2 Sqrt[1 + #1 + #1^2]] + #1 + Sqrt[
     1 + #1 + #1^2] &][x + 1/2 (2 + 2 Sqrt[7] - 4 Log[-2 + Sqrt[7]] + 
      3 Log[-5 + 2 Sqrt[7]])]

Let us verify the accuracy.

i. Generate log-mesh for plotting purposes. Represent only 20 points in the range $[1, 10000]$

kmx = 20;
nmx = 100000;
p = Exp[Log[nmx]/kmx] // N
ni = Table[t = Round[p^(i - 1)]; t, {i, 1, kmx}] // DeleteDuplicates

ii. Generate the solution of the 2nd recursion.

a = {2};
Do[AppendTo[a, x = Last[a]; N[Sqrt[x^2 + x + 1]]], {n, nmx}]
an = Table[{i, a[[i]]}, {i, ni}]

iii. Generate the solution of the 1st recursion.

u = {1};
Do[AppendTo[u, x = Last[u]; N[x + 1 + Sqrt[x + 3]]], {n, nmx}]
un = Table[{i, u[[i]]}, {i, ni}]

iv. Plot 2nd recursion vs analytic solution

g1 = LogLogPlot[f[n], {n, 1, nmx}];
g2 = ListLogLogPlot[an, 
  PlotStyle -> Directive[PointSize[Medium], Orange]];
Show[{g1, g2}]

And here is the same graph with the polynomial asymptotic.

v. Plot 1st recursion vs analytic solution

g3 = LogLogPlot[f[n]^2 - 3, {n, 1, nmx},PlotTheme -> "NeonColor"];
g4 = ListLogLogPlot[un, 
  PlotStyle -> Directive[PointSize[Medium], Blue]];
Show[{g3, g4}]

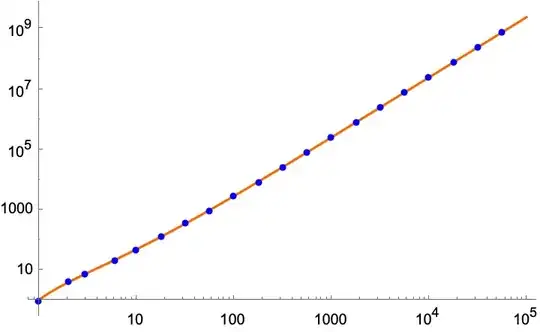
And here is the same graph with the polynomial asymptotic.

Finally, in the case someone needs a practical formula working in the whole range. One can transform the original recursion into a differential equation with the solution

v[n_] := -2 + 2 ProductLog[-1, -3 E^(-(5/2) - n/2)] + 
  ProductLog[-1, -3 E^(-(5/2) - n/2)]^2

Using properties of the Lambert W function one can with high accuracy write

g[n_] := Log[3 E^(-(5/2) - n/2)] - Log[5/2 + n/2 - Log[3]] + 
  Log[5/2 + n/2 - Log[3]]/Log[3 E^(-(5/2) - n/2)] + (Log[5/2 + n/2 - Log[3]]*(Log[5/2 + n/2 - Log[3]] - 2))/(2* Log[3 E^(-(5/2) - n/2)]^2)
w[n_] := -2 + 2*g[n] + g[n]^2

This function has the following asymptotic form

wa[n_]:=1/4 (-3 + n (6 + n)) - (3 + n) Log[3] + Log[3]^2

Answer 2

We can find an asymptotic solution by

AsymptoticRSolveValue[{u[n + 1] == u[n] + 1 + Sqrt[u[n] + 3],   u[1] == 1}, u[n], {n ,Infinity,3}]

6 - 6 n + n^2

Addition. The result of

nl = NestList[# + 1 + Sqrt[3 + #] &, 1.000000000000,  10^5];
 fL = #^2 - 6 # + 5 & /@ (Range@Length@nl); ListPlot[{fL/nl}]

suggests that the result of AsymptoticRSolve has the correct order of the growth up to the multiplier 1/4.

Let us find an asymptotic solution of {u[n + 1] == u[n] + 1 + Sqrt[u[n] + 3], u[1] == 1} in the form u[n_] := a*n^2 + b*n + c.

We substitute it in the recurrence equation and find the asmptotic at infinity by

Series[u[n + 1] - u[n] - 1 - Sqrt[u[n] + 3], {n, Infinity, 3}, 
Assumptions -> {a, b, c} \[Element] Reals && n > 1] // Normal

-1 + a + b - b/( 2 Sqrt[a]) + ((12 a - 5 b^2 + 4 a c) (12 a - b^2 + 4 a c))/( 128 a^(7/2) n^3) + (b (12 a - b^2 + 4 a c))/( 16 a^(5/2) n^2) + (-12 a + b^2 - 4 a c)/( 8 a^(3/2) n) + (-Sqrt[a] + 2 a) n

We want to cancel as many as possible terms in the above.

Solve[-Sqrt[a] + 2 a == 0, a, Reals]

gives a -> 1/4, The term -1 + a + b - b/( 2 Sqrt[a])==-3/4 cannot be cancelled. Now

Solve[{0 == -12 a + b^2 - 4 a c, 12 a - 5 b^2 + 4 a c == 0} /. 
a -> 1/4, {b, c}, Reals]

{{b -> 0, c -> -3}}

Hence, we draw the conclusion that u[n_]:=1/4*n^2-3 can be taken as an asymptotic solution.