1

Refine works with symbols in either way:

Refine[Sqrt[x^2], Element[x, Reals]]
(* Abs[x] *)

Refine[Sqrt[x^2], x > 0]
(* x *)

But assuming positive-valued arbitrary function f[x] does not work. (Real-valued f[x] works, though.)

Refine[Sqrt[f[x]^2], Element[f[_], Reals]] (*Works*)
(* Abs[f[x]] *)

Refine[Sqrt[f[x]^2], f[_] > 0] (Does not work)
(* Sqrt[f[x]^2] *)

How can I correctly assume that f is a positive-valued unary function?

xzczd
  • 65,995
  • 9
  • 163
  • 468
JS S
  • 121
  • 2

3 Answers3

1

As mentioned in e.g. this and this post:

Though pattern matching seems to work in $Assumption/Assumption in some cases, one should avoid making use of this undocumented feature coincidence, because it's rather unstable.

In OP's case, the only correct way to assume f is a positive-valued unary function I can think out is as follows:

(* Let's use a more general expression as example: *)
expr = Sum[Sqrt[f[Subscript[x, i]]^2], {i, 5}]

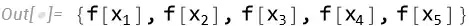
enter image description here

lst = Union@Cases[expr, f[_], Infinity]

enter image description here

assume = Table[var > 0, {var, lst}]

enter image description here

Refine[expr, assume]

enter image description here

xzczd
  • 65,995
  • 9
  • 163
  • 468
1

Using Assuming and Refine:

Assuming[Thread[Cases[#, f[_], Depth@#] > 0] &@#, Refine[#]] &@expr

enter image description here

E. Chan-López
  • 23,117
  • 3
  • 21
  • 44
-1
  Assuming[f[_]>0, PowerExpand [Sqrt[f[x]^2] ]

It seems that the special task of the evaluation of nested powers is contained in PowerExpand.

Mathematica e.g. refrains from adding logs. The reason may be that simple formulas exist on Riemann surfaces only. The usual technique to cut a sheet off the Riemann surfaces as part of the complex plane is to a great part logically not extendable to a greater domain than just real positive maps $f: \mathbb R_+\to \mathbb R_+$

Roland F
  • 3,534
  • 1
  • 2
  • 10
  • 3
    The Assuming is not doing anything. You get the same result with just PowerExpand[Sqrt[f[x]^2]] – Bob Hanlon Nov 29 '23 at 15:46
  • True, but in most times the simplifying procedures contain more operations and its good practice to define domains. – Roland F Nov 29 '23 at 18:09
  • 2
    Let me make the issue clearer: Assuming[f[_] < 0, PowerExpand[Sqrt[f[x]^2]]] still gives f[x] as output. This is because the default option value of Assumptions of PowerExpand is not $Assumptions but Automatic, while Assuming only influences value of $Assumptions. (See Details section of document of PowerExpand for more info. ) BTW, if you write PowerExpand[Sqrt[f[x]^2], Assumptions -> f[_] < 0], the output will be E^(I \[Pi] Floor[1/2 - Arg[f[x]]/\[Pi]]) f[x], still undesired. – xzczd Dec 01 '23 at 00:59